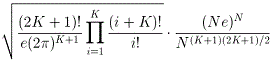Multimagic series for squares
See also
the multimagic series for cubes
As we have seen for the smallest bimagic and
the smallest trimagic squares,
it may be interesting, in order to try to construct a p-multimagic square of
order-n, to find all the p-multimagic series of order n, that is to say the
series of n different integers, from 1 to n², having the correct magic, bimagic,...
up to p-multimagic sums.
The order 4 is the smallest order allowing us to get a bimagic series.
Here are the 2 bimagic series, which are also surprisingly trimagic:
This means that:
- 15 + 9 + 8 + 2 = 14 + 12 + 5 + 3 = 34 = S1
- 152 + 92 + 82 + 22 = 142 + 122 + 52 + 32 = 374 = S2
- 153 + 93 + 83 + 23 = 143 + 123 + 53 + 33 = 4624 = S3
For the order 5, there are 8 bimagic series for which the list is
given in the Smallest bimagic square page.
Here is a summary of the number of multimagic series. Some of these lists are downloadable as Excel files, from 28Kb to 800Kb each.
For order 12, the numbers of the trimagic, tetramagic and pentamagic series
were kindly communicated by Walter Trump,
Germany. In 2004, the numbers of Walter Trump were confirmed by Fredrik Jansson,
Finland. And Fredrik goes further: he is the first to have computed the
huge number of bimagic series of order 12, and the number of multimagic series
of order 13 (excepted bimagic series of order 13).
New steps on bimagic series, between July and October 2005, from Germany:
- With a new method, Lorenz Schlangen is the first to compute the
numbers of bimagic series of orders 13, 14 and 15
- Walter confirms, some weeks after Lorenz, and using Lorenz's new
method (but a different program), the three numbers
- And Walter goes further: with the same new method, he is the first to
compute the numbers of bimagic series of orders 16 and 17
In April 2008, Michael Quist, USA, computed the numbers of tetramagic and
pentamagic series of order 16. In May 2008, he computed the number of trimagic
series of order 15 (and also confirmed the number of trimagic series of
order 13 previously computed by Fredrik Jansson). In August 2008, he computed
the number of bimagic series of orders 18, 19 and 20 (and also confirmed the
number of bimagic series of smaller orders previously computed). In May 2013,
he computed
the number of bimagic series of orders 21, 22, 23, numbers independently computed and
confirmed a few days later by Lee Morgenstern, USA. Then in May and June 2013,
directly using the software written by Lee Morgenstern (PDF
with counting
method by L. Morgenstern), Walter Trump computed
the number of bimagic series of orders 24, 25, 26, 27 and 28. In December
2014, Lee Morgenstern computed the number of trimagic series of orders 16 and
17. In August 2015, Dirk Kinnaes, Belgium, confirmed the previously known
numbers of bimagic series, and computed the numbers of bimagic series of orders
29 and 30 (PDF with algorithm
by D. Kinnaes).
Number of multimagic series for squares
(click on the cells
to download the corresponding Excel files)
|
Order
|
Bimagic
|
Trimagic
|
Tetramagic
|
Pentamagic
|
Hexamagic
|
|
3
|
0
|
0
|
0
|
0
|
0
|
|
4
|
2
|
2
|
0
|
0
|
0
|
|
5
|
8
|
2
|
0
|
0
|
0
|
|
6
|
98
|
(a)
0
|
0
|
0
|
0
|
|
7
|
1844
|
0
|
0
|
0
|
0
|
|
8
|
38039
|
121
|
0
|
0
|
0
|
|
9
|
949738
|
126
|
0
|
0
|
0
|
|
10
|
24643236
|
(a)
0
|
0
|
0
|
0
|
|
11
|
947689757
|
31187
|
0
|
0
|
0
|
|
12
|
45828982764
|
2226896
|
106
|
4
|
0
|
|
13
|
2151748695931
|
17265701
|
555
|
3
|
0
|
|
14
|
123821075526032 |
(a)
0
|
0
|
0
|
0
|
|
15
|
8131094055190149 |
69303997733 |
(b)(c)
0
|
0
|
0
|
|
16
|
573957471153552576
|
1683487116508
|
235275
|
13
|
0
|
|
17
|
44010987379157415768
|
112205432382966
|
(c) 0
|
0
|
(f)(g) 0
|
|
18
|
3655486139293429450720 |
(a)
0
|
0
|
0
|
0
|
|
19
|
333633403912637510806972 |
Unknown! (h) ~ 2.00 · 1017
|
Unknown! (d) > 0
|
(e) 0
|
(f)(g) 0
|
|
20
|
32862657239386515532593520
|
Unknown! (h) ~ 1.41 · 1019
|
Unknown! (d) > 0
|
Unknown! (d) > 0
|
(g) 0
|
|
21
|
3431453899306300581868236386
|
Unknown! (h) ~ 1.08 · 1021
|
Unknown! (d) > 0
|
Unknown! (d) > 0
|
(g) 0
|
|
22
|
384125946998166710305616659402
|
(a)
0
|
0
|
0
|
0
|
|
23
|
45801639842337348432002857205878
|
Unknown! (h) ~ 7.96 · 1024
|
Unknown! (d) > 0
|
(e) 0
|
(g) 0
|
|
24
|
5773407884408951768360741341457291
|
Unknown! (h) ~ 7.61 · 1026
|
Unknown! (d) > 0
|
Unknown! (d) > 0
|
(g) 0
|
|
25
|
768467875608077797720790265285636797
|
Unknown! (h) ~ 7.78 · 1028
|
Unknown! (d) > 0
|
(e) 0
|
(g) 0
|
|
26
|
107710220763567919574782844625088827344
|
(a)
0
|
0
|
0
|
0
|
|
27
|
15880475347526962316266889239839811859979
|
Unknown! (h) ~ 9.78 · 1032
|
Unknown! (i) > 0
|
Unknown! (i) > 0
|
Unknown!!!!!!
|
|
28
|
2455456581123976779162274548131606029110869
|
Unknown! (h) ~ 1.19 · 1035
|
Unknown! (d) > 0
|
Unknown! (d) > 0
|
(g) 0
|
|
29
|
397017067970073855910942668942599683652058914
|
Unknown! (h) ~ 1.54 · 1037
|
Unknown! (d) > 0
|
Unknown! (d) > 0
|
(g) 0
|
|
30
|
67063309991205148544594890672812817873237628826
|
(a)
0
|
0
|
0
|
0
|
|
31
|
Unknown! (h) ~ 1.181 · 1049
|
Unknown! (h) ~ 2.97 · 1041
|
Unknown!!!!!!
|
(j) 0
|
(g) 0
|
|
32
|
Unknown! (h) ~ 2.165 · 1051
|
Unknown! (h) ~ 4.43 · 1043
|
Unknown! (d) > 0
|
Unknown! (d) > 0
|
(g) 0
|
(a) Trimagic series of order 4k+2 are impossible: it is
impossible to have S3 even, with S1 odd and S2 odd.
(b) Tetramagic
series of order 15 are impossible: see below the proof by Robert Gerbicz, Hungary, in 2006.
(c) Tetramagic
series of orders 15 and 17 are impossible: see below the proofs by
Lee Morgenstern, USA, in 2013
(d) These tetramagic and pentamagic
series are difficult to find, but are possible: see below the examples by Lee Morgenstern, in 2013
(e) Pentamagic series of
orders 19, 23 and 25 are impossible: see below the proofs
by Lee Morgenstern, in 2013
(f) Hexamagic
series of orders 17 and 19 are impossible: see below the proofs by Jaroslaw Wroblewski, Poland, in 2008.
(g)
Hexamagic series of orders from 12 to 39 (excepted the unknown order
27) are impossible: see below the proofs by Lee Morgenstern, in
2013.
(h) Estimations
of bimagic and trimagic series, see below the formulas by Michael Quist,
2013.
(i) Pentamagic series of order 27 are possible: see below the
examples by Christian Boyer and Lee Morgenstern,
in 2013.
(j) Pentamagic series of order 31 are impossible: see below
the proof by Jean Moreau de Saint-Martin,
in 2013.
The order 12 is the smallest order allowing tetra and pentamagic
series. In the 106 tetramagic series, 4 of them are also pentamagic. These 4
series are symmetrical left/right, that is to say that i-th number + (13-i)th number = 12² + 1 = 145.
- 143 116 109 108 100 85 60 45 37 36 29 2
- 140 124 117 97 90 89 56 55 48 28 21 5
- 137 127 121 100 81 80 65 64 45 24 18 8
- 135 129 123 95 86 78 67 59 50 22 16 10
What is the smallest order allowing hexamagic series? The smallest current
candidates are orders 27 and 40.
The bimagic, trimagic, tetramagic and pentamagic series are referenced respectively under the
numbers A052457, A052458, A090037
and A106646
in the On-Line Encyclopedia of Integer Sequences, OEIS
Foundation.
See also the "Multimagic
Series" topic in the Eric Weisstein's
World of Mathematics, Wolfram Research.
In April-May 2005, Walter Trump computed an estimation of the number of various
magic series, including bimagic series from order 13 to order 20, using
Monte Carlo methods. More details at www.trump.de/magic-squares/magic-series/multi.htm.
The true numbers of bimagic series, computed after his estimation (see
above), are very close: his estimation method has proved excellent!
Numbers of bimagic series, estimated by Walter Trump. Comparison
with the true numbers.
|
Order
|
Estimated number
|
True number
|
Error
|
|
13
|
2.16 · 1012
|
2151748695931
|
+0.39%
|
|
14
|
1.24 · 1014
|
123821075526032 |
+0.14%
|
|
15
|
8.15 · 1015
|
8131094055190149 |
+0.23%
|
|
16
|
5.74 · 1017
|
573957471153552576
|
+0.01%
|
|
17
|
4.41 · 1019 |
44010987379157415768
|
+0.20%
|
|
18
|
3.65 · 1021 |
3655486139293429450720 |
-0.15%
|
|
19
|
3.33 · 1023 |
333633403912637510806972 |
-0.19%
|
|
20
|
3.29 · 1025 |
32862657239386515532593520
|
+0.11%
|
In June 2013, Michael Quist wrote a paper estimating the
numbers of magic and multimagic
series,
including bimagic series for squares of order N. See http://arxiv.org/abs/1306.0616.
Here is his formula, and the
numeric values obtained for 20 ≤ N ≤ 30. The error decreases with
higher orders. In August 2015, Dirk Kinnaes improved Quist's formula,
adding a new term (see also his PDF given above).
Estimated numbers of bimagic series, formula by Michael
Quist:
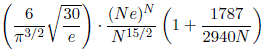
Improved
adding + 11522051 / 70630560N² term, by Dirk Kinnaes.
Comparison with the true numbers.
Order | Quist
estimated number | Kinnaes
estimated number | True number | Quist
error | Kinnaes
error |
20 | 3.27798 · 1025 | 3.27668 · 1025 | 32862657239386515532593520
| -0.2521% | -0.2916% |
21 | 3.43856 · 1027 |
3.43732 · 1027 |
3431453899306300581868236386
| +0.2070% | +0.1710% |
... | ... |
... |
... |
... |
... |
27 | 1.58874 · 1040 |
1.58839 · 1040 |
15880475347526962316266889239839811859979
|
+0.0436%
|
+0.0217%
|
28 | 2.45557 · 1042 |
2.45507 · 1042 |
2455456581123976779162274548131606029110869
|
+0.0045%
|
-0.0159%
|
29 | 3.97141 · 1044 |
3.97066 · 1044 |
397017067970073855910942668942599683652058914
|
+0.0313%
|
+0.0123%
|
30 | 6.70832 · 1046 |
6.70713 · 1046 |
67063309991205148544594890672812817873237628826
|
+0.0296%
|
+0.0119%
|
31 | 1.18141 · 1049 |
1.18122 · 1049 |
?
|
?
|
?
|
32 | 2.16576 · 1051 |
2.16542 · 1051 |
?
|
?
|
?
|
Not in his paper, but in May 2013 Michael Quist calculated this other
formula:
The numbers estimated by this formula, for N > 18, are in the trimagic
column of the first table
of this page.
And in December 2013, he proposed this general formula for
multimagic series of order N (the trimagic formula above can be obtained
with K=3):
In January 2006, Robert Gerbicz, Hungary, proved
that there is no tetramagic series of order 15. Here is his proof.
The magic
sums are:
- S1=1695
- S2=254815
- S3=43095375
- S4=7774354687
S4==15
mod 16. Because (2x+1)^4==1 mod 16 and (2x)^4==0
mod 16, all 15 numbers have to be odd.
Let a(k)=2b(k)+1 (where every b(k) is an integer) and
T1=sum(b(k), k=1..15), T2=sum(b(k)^2, k=1..15), and so on...
From the binomial
theorem we have:
- S1=sum(2b(k)+1, k=1..15) = 2*T1+15 = 1695
- S2=sum((2b(k)+1)^2, k=1..15) = 4*T2+4*T1+15 = 254815
- S3=sum((2b(k)+1)^3, k=1..15) = 8*T3+12*T2+6*T1+15 = 43095375
- S4=sum((2b(k)+1)^4, k=1..15) = 16*T4+32*T3+24*T2+8*T1+15 = 7774354687
It is
easy to solve this linear system of equations:
- T1=840
- T2=62860
- T3=5292000
- T4=475218457
There is a contradiction. Because x==x^4 mod
2, we should have T1==T4 mod 2: but T1 is even and T4 is odd!
So there is no
tetramagic (and pentamagic, hexamagic...) series for squares of order 15.
In July 2008, Jaroslaw Wroblewski, Poland, proved
that there is no hexamagic series of order 17. Here is his proof.
From S4=1(mod 17) we conclude that the series
must contain 17 odd terms or one odd term and 16 even terms.
***** In case of 17 odd terms, each of the
form 4k+1 (where k may be negative)(*), after denoting by Ki the sum of i-th powers
of k's, we get
- S2 = 475745 = 16 K2 + 4 K1 + 17
- S4 = 23923217921 = 256 K4 + 256 K3 + 96
K2 + 16 K1 + 17
which leads to
- 59466 = K1 + 2 K2
- 1495201119 = K1 + 6 K2 + 16 K3 + 16 K4
giving a contradiction on parity of K1. There
are no tetramagic series in this case.
***** In case of 1 odd term of the form 4k+1
(where k may be negative) and 16 even terms of the form 2p, after denoting by
Pi the sum of i-th powers of p's, we get from equations on S2 and S4 respectively:
- 118936 = 2 k + 4 k^2 + P2
- 1495201120 = k + 6 k^2 + 16 k^3 + 16 k^4
+ P4
As P2 and P4 have the same parity, k must be
even, say k = 2m. We get from equation on S6:
- 89508435052624 = 3 m + terms_divisible_by_4
which allows us to write m=4r. We get from
equation on S2 and S6:
- 118936 = P2 + 16 r + 256 r^2
- 22377108763156 = P6 + 3 r + terms_divisible_by_8
Since P2=P6(mod 4), we can take r=4q. At this
point the odd term of the magic series is equal to 128q+1, q = -2,-1,0,1,2.
From the equation on S4, which takes form
- 1495201120 = P4 + 32 q + 6144 q^2 + 524288
q^3 + 16777216 q^4
we conclude that P4 is divisible by 32 and
in view of P4 = P6 (mod 8), P6 is divisible by 8.
Equation on S6 gives:
- 22377108763156 = P6 + 12 q + terms_divisible_by_8
This forces q to be odd, i.e. q must be plus
or minus 1.
In case q=1 we get:
- P2 = 114776
- P4 = 1477893440
- P6 = 22305104487176
In case q=-1 we get:
- P2 = 114904
- P4 = 1478942080
- P6 = 22311548248864
In either case P4 is divisible by 16, which
means that all p's are odd or all are even. However P6 is not divisible by 64,
which rules out the possibility of all even p's. Let p=4x+1 (x being integer of
any sign).
From equations on S2 and S4 we get for
q=1:
- 14345 = X1 + 2 X2
- 92368339 = X1 + 6 X2 + 16 X3 + 16 X4
and for q=-1:
- 14361 = X1 + 2 X2
- 92433879 = X1 + 6 X2 + 16 X3 + 16 X4
In both cases there is mod 4 contradiction.
And again in July 2008, Jaroslaw Wroblewski proved that there is no hexamagic
series of order 19. Here is his proof.
S4(mod 16)=7, implies that each series must
have 7 odd and 12 even terms, of the form 4k+1 and 2p respectively. Then
equations on S2, S4, S6 give:
- 207198 = 2 K1 + 4 K2 + P2
- 4061581299 = K1 + 6 K2 + 16 K3 +
16 K4 + P4
- 758246942365254 = 3 K1 + 30 K2 +
160 K3 + 480 K4 + 768 K5 + 512 K6 + 8 P6
The last equation gives even K1 and then P2 and
P4 get contradictory parity, which proves there are no hexamagic series of order
19.
(*) About odd terms of the form 4k+1 "WHERE k MAY BE
NEGATIVE". Yes, each odd integer, or its opposite, is of the form 4k+1:
- 1 = 4*0+1
- -3 = 4*(-1)+1
- 5 = 4*1+1
- -7 = 4*(-2)+1
- 9 = 4*2+1
- -11 = 4*(-3)+1
and so on, with k = 0, -1, 1, -2, 2, -3,... Nice trick!
From March to August 2013, Lee Morgenstern
proved that there is no tetramagic series of orders 3, 4, 5, 7, 8, 9, 11, 15
and 17. Proved that there is no pentamagic series of orders 19, 23 and 25. And proved that there is no hexamagic series of orders 12, 13, 16, 19,
20, 21, 23, 24, 25, 28, 29, 31, 32, 33, 35, 36, 37 and 39.
The existence of
hexamagic series of orders 27 and 40 (and numerous >40) is unknown.
In July and August 2013, he proved that some multimagic series exist, finding these
examples:
- Tetramagic 19, with (316, 315,
314, 313, 311, 309, 230, 206, 173, 146, 142, 131, 126, 116, 110, 107, 64,
8, 2)
- Pentamagic 20, with (400, 383, 311, 302, 294, 287,
281, 276, 274, 263, 138, 127, 125, 120, 114, 107, 99, 90, 18, 1)
- Pentamagic 21, with (437, 429, 346, 336, 332, 331, 321,
302, 298, 288, 221, 154, 144, 140, 121, 111, 110, 106, 96, 13, 5)
- Tetramagic 23, with (514, 499, 459, 454, 439, 427, 379,
319, 314, 307, 283, 274, 259, 223, 211, 199, 139, 124, 94, 64, 49, 34, 31)
- Pentamagic 24, with (576, 569, 467, 453, 435, 425,
414, 411, 404, 397, 394, 355, 222, 183, 180, 173, 166, 163, 152, 142, 124,
110, 8, 1)
- Tetramagic 25, with (559, 558, 556, 554, 551, 544,
524, 433, 409, 341, 337, 313, 304, 277, 253, 229, 217, 196, 181, 157, 153,
109, 49, 12, 9)
In October 2013, Christian Boyer found this symmetrical
family:
- Pentamagic 27, with (35, 42, 45, 99, 105, a,
190, b, 245, 275, 289,
c, 361, 365, 369, 730-c,
441, 455, 485, 730-b,
540, 730-a, 625, 631,
685, 688, 695)
- (a,
b, c)
= (133, 203, 295), or (135, 197, 303), or (155, 163, 357).
and from Lee Morgenstern:
- Pentamagic 27, with (729, 720, 605, 601, 575, 573,
553, 549, 545, 505, 473, 430, 405, 365, 325, 300, 257, 225, 185, 181, 177,
157, 155, 129, 125, 10, 1)
- Pentamagic 28, with (710, 709, 708, 707, 706, 704,
679, 523, 476, 471, 466, 444, 426, 423, 362, 359, 341, 319, 314, 309, 262,
106, 81, 79, 78, 77, 76, 75)
- Pentamagic 29, with (799, 798, 797, 795, 658, 628,
622, 604, 592, 578, 574, 570, 547, 430, 421, 412, 295, 272, 268, 264, 250,
238, 220, 214, 184, 47, 45, 44, 43)
- Pentamagic 32, with (931, 930, 929, 928, 927, 926,
924, 826, 697, 643, 628, 612, 607, 598, 552, 517, 508, 473, 427, 418, 413,
397, 382, 328, 199, 101, 99, 98, 97, 96, 95, 94)
- Pentamagic 40, with (1431, 1430, 1429, 1428,
1427, 1426, 1424, 1423, 1421, 1420, 1374, 891, 867, 864, 860, 859, 838, 828, 825, 804,
797, 776, 773, 763, 742, 741, 737, 734, 710, 227,
181, 180, 178, 177, 175, 174, 173, 172, 171, 170)
In September-October 2013, Jean Moreau de Saint-Martin,
France, studied and checked in detail Morgenstern's mathematical proofs on multimagic
series (from the above zipped text files), and found no error.
And he went further, simplifying and generalizing Morgenstern's proofs.
Also using some of my remarks and computations, we now have new impossibility proofs:
- Pentamagic series of order 31 are impossible
- Hexamagic series of orders 43, 44, 47, 48, 49, 52, 60, 63, 65 are impossible
Here is this study on multimagic series:
In February 2017, Lee Morgenstern recaped his
updated numerous proofs
on multimagic series up to order 44, and up to octamagic. His remark:
"Of importance are the mathematical proofs for
order 7 trimagic and order 16 hexamagic because they use unique proof techniques.
Perhaps someone can use these to attack order 27 hexamagic."
Return to the home page http://www.multimagie.com