Enigmas on Magic Squares: win €8,000 and 12 bottles of champagne!!!

While magic squares have been known and studied for many centuries, it is surprising that for certain types of magic squares we still do not know today which are the smallest possible! In an effort to make progress on these unsolved problems, twelve prizes totaling €8,000 and 12 bottles of champagne are offered for the solutions to twelve enigmas (six main at €1,000 each, six small from €100 to €500 each):

With the solutions of enigmas #3a, #4c, #5 and #6b, there still remain eight prizes totaling €6,500 + eight bottles of champagne (at the time of the last update of this website). Since all the enigmas on 7x7 squares are now solved, the remaining enigmas are on small squares, from 3x3 to 6x6.

Who can construct, or prove the impossibility:

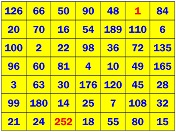
  1. 3x3 magic square using 7 (or why not 8, or 9) distinct squared integers different from this only known example (and of its rotations, symmetries and k² multiples):

      2. 373²

      289²

      565²

      360721

      425²

      23²

      205²

      527²

      222121
  2. 5x5 bimagic square using distinct positive integers
  3. 3x3 semi-magic square of cubes using distinct positive cubed integers (small enigma #3a: square 7x7)
  4. 4x4 magic square of cubes using distinct positive cubed integers (small enigmas #4a, #4b, #4c: squares 5x5, 6x6, 7x7)
  5. multiplicative magic cube using distinct positive integers < 364
  6. 5x5 additive-multiplicative magic square using distinct positive integers (small enigmas #6a , #6b: squares 6x6, 7x7)

No, I myself do not have the solutions... Of course, only the first person who solves an enigma will win the associated prize and will be named in this table:

Important remark on the main enigma #1. Strictly speaking, an impossibility proof of 8 or 9 distinct squared integers in a 3x3 magic square is not a solution, because another 3x3 magic square using 7 squared integers remains (perhaps) possible. However, because such an impossibility proof would be an impressive result, it will be rewarded by a prize: €500 + bottle of champagne.

Winners
  • Congratulations to Toshihiro Shirakawa, Japan, who, very quickly after the announcement of the contest on April 6th, 2010, solved two enigmas:
    #5 as soon as April 15th with his cube, then #3a one week later, April 22nd, with his square

    • Here happy, with his first bottle of champagne! He received a second one, some days later. A total of two Moët & Chandon impérial bottles, and of €1100.

 

 

 
  • Congratulations to Sébastien Miquel, France, who solved the enigma #4c, February 20th, 2015,
    with his square 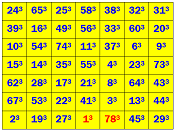and so won a bottle and €200.


C. Boyer & S. Miquel
(Paris, March 2015)

 

 

  • A year and a half later, congratulations again to Sébastien Miquel, who solved the enigma #6b, August 15th, 2016,
    with his square and so won again a bottle and €200.

    • Who will be the next winner? With which enigma?


C. Boyer & S. Miquel
(Paris, September 2016)

Enigmas in Pour La Science... and elsewhere

                                        in
Dossier Pour La Science (Jeux math')....... and Pour La Science website

Many thanks to the numerous people, magazines and websites for announcing the contest after receiving the press release sent April 6th 2010, in particular, in chronological order:

In advance, sorry to others of whom I am not aware, but I also thank them!

And also, for reporting the solutions found by Toshihiro Shirakawa, thanks to:

With this Japanese paper in Sugaku Seminar, I know now that my name is written that way in katakana:

Thanks to Toshihiro for identifying the characters of my name. Amusing: the numbers being the only characters that we can easily read, we may deduct that this paragraph probably says that in 2010, in April (4), I submitted 12 enigmas, prizes totaling 8000 euros, each being from 100 to 1000 euros. Am I right?

Thanks for their report of the solution of #4c found by Sébastien Miquel:

Thanks for their report of the solution of #6b found by Sébastien Miquel:

Return to the home page http://www.multimagie.com