Multiplicative magic cubes

What are multiplicative magic cubes?

Multiplicative magic cubes are cubes which are magic using multiplication instead of addition. The numbers used can't be consecutive, but they must be distinct. A reminder of some definitions, similar to additive cubes:

It seems that the first multiplicative magic cubes were published in 1913 by Harry A. Sayles in The Monist in 1913. This paper was republished in the book Magic squares and cubes by W.S. Andrews, where we can find (page 293) two cubes:

In 2002, Marián Trenkler, Slovakia, published a paper on multiplicative magic squares and cubes in Obzory Matematiky, Fyziky a Informatiky 1/2002 (31), pages 9-16, with:

Is it possible to do better? Cube of the same orders, but using smaller products P, or smaller Max nb? Yes, both for the orders 4 and 5!

After multiplicative magic squares, here are the best known cubes, 3rd-order to 11th-order. The goal is always to minimize the magic product and the max nb.

Many thanks to Edwin Clark, Mathematics Department of the University of South Florida, USA, for checking in 2006 all my multiplicative cubes, confirming that they have all the announced properties.

3rd-order multiplicative magic cubes

It is easy to prove that any 3rd-order multiplicative magic cube must have P = (center)^3. With two different possible constructions using the integer 1

we can produce exactly 4 different 3rd-order multiplicative magic cubes with the same P = (2·3·5)^3 = 27000: one cube from the first construction, and three from the second construction. They use the same set of integers, but they are "different" because from any of these 4 cubes, it is impossible to produce any other ones, using symmetries and rotations.

It is impossible to construct better 3rd-order cubes with a smaller P. But, using Min nb > 1, it is possible to construct 3rd-order cubes with a smaller Max nb (and bigger P), the smallest possible Max nb being 400. Here are some examples with Max nb < 900:

And it is possible to construct 3rd-order semi-magic cubes using smaller constants. In the three examples below, all the rows, columns and pillars have the same magic product P = 7560, but some of their 4 triagonals do not have the same product: the example on the right is a very nearly magic cube, only one triagonal is incorrect!!!

In February 2013, André LFS Bacci, Brasilia, Brazil, constructed this semi-magic cube with a smaller P:

In June 2017, I was surprised to receive still better 3rd-order semi-magic cubes! From Elbert Krison, a 15-year-old schoolboy of Jakarta, Indonesia. Elbert sent also new best known magic cubes of orders 8 to 11 listed in the table.

And what about adding magic plane diagonals? Both for additive and multiplicative magic cubes, it is impossible to construct 3rd-order perfect magic cubes.

4th-order multiplicative magic cubes

Sayles's cube and Trenkler's cube have the same characteristics: P = 57153600, Max nb = 7560. Is it possible to construct 4th-order cubes with smaller constants? Yes! My best cubes have a P more than 8 times smaller, and a Max nb more than 20 times smaller:

4th-order multiplicative magic cubes, by Christian Boyer
P = 6,486,480 and Max nb = 546 (left cube, January 2006),
P = 17,297,280 and Max nb = 364 (right cube, June 2007)
(click on the image to enlarge a cube)

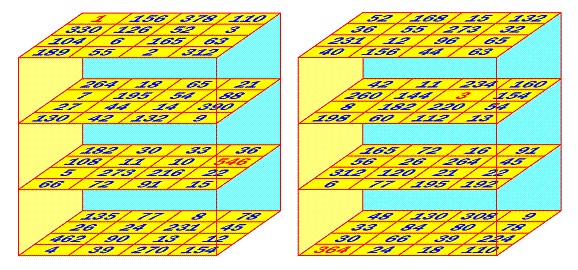
Some plane diagonals of my two cubes are magic, but not all of them: both for additive and multiplicative magic cubes, it is impossible to construct 4th-order perfect magic cubes.

These were my two best cubes, but not sure I found the best possible cubes. That's why I asked these next questions. Who will be able to construct better 4th-order cubes (with smaller P or smaller Max nb)?  Is it possible to construct a multiplicative magic cube (of any order!) using integers < 364? Of any order, because we can notice that the Max nb = 364 of the 4th-order cube on the right is smaller than the Max nb = 400 used for the best possible 3rd-order cube.

In July 2008, Michael Quist worked on this problem, and found that any 4th-order cube must have Max nb ≥ 221 and that any 5th-order (or higher) cube must have Max nb ≥ 442. If we suppose that his work is correct (read it here), and if we suppose that any 3rd-order cube must have Max nb ≥ 400, then the enigma is limited to the 4th-order, and is equivalent to: is it possible to construct a multiplicative magic cube, of 4th order, and having 221 ≤ Max nb < 364?

In January 2010, Max Alekseyev, Dept of Computer Science & Engineering, University of South Carolina, found another 4th-order magic cube having the same Max nb = 364 as my above cube, but with a smaller P. None of its 24 small diagonals are magic (8 small diagonals are magic in my cube), but this is not a problem because not needed in a magic cube: only rows + columns + pillars + 4 triagonals have to be magic. An excellent cube constructed by Max!

Toshiro Shirakawa in 2010 (Kuwana, Japan, 1983 - )

And finally in April 2010, Toshihiro Shirakawa solved my enigma #5 with this excellent cube using smaller integers: Max nb = 351 < 364. The magic product is also smaller than the above cubes. Congratulations!!! Toshihiro lives in Ebina Kanagawa, Japan. He is a programmer, and does mathematics as a hobby.

April 2010. Best known 4th-order multiplicative magic cube, by Toshihiro Shirakawa
and best known cube -of any order- using the smallest possible integers
P = 4,324,320 and Max nb = 351
(click on the image to enlarge it)
 

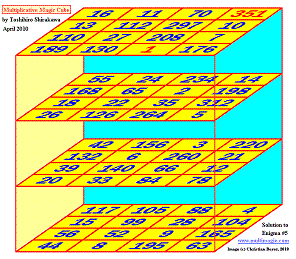
His method is easy and ingenious, without any computing. He used, directly from this website, my own 4x4 multiplicative semi-magic square having the smallest possible product that I constructed in 2005, with magic product 4320 = 25 * 33 * 5 and Max nb 27:

Noticing that this square used only factors 2, 3 and 5, he cleverly reused it, combined with the four factors (E, F, G, H) = (1, 11, 7, 13). That's why his magic product is 4320(from the square) *7*11*13(his factors) = 4324320, and his Max nb is 27(from the square) * 13(his max factor) = 351. And 351 is less than 364, as asked in the enigma. That's it! Er... shame on me... to have been unable to think to this ingenious method... using my own square...

I can now give the method used for my cube (P, MaxNb) = (17297280, 364) which was challenged with enigma #5. This cube was constructed from the Eulerian (or Graeco-Latin) cube below, using the best possible set (A, B, C, D) (I, J, K, L) (a, b, c, d) generating 64 distinct integers and generating the smallest MaxNb:

My other cube (P, MaxNb) = (6486480, 546) used a similar Eulerian cube, but with the best possible set generating 64 distinct integers and generating the smallest product: (1, 2, 3, 6), (1, 4, 5, 7), (1, 9, 11, 13).

5th-order multiplicative magic cubes

Trenkler's cube published in 2002 has P = 35286451200, Max nb = 2448. Is it possible to construct 5th-order cubes with smaller constants? Yes! My best cube has a P more than 2 times smaller, and a Max nb more than 2 times smaller:

January 2006: 5th-order multiplicative magic cube, by Christian Boyer
P = 16,761,064,320 and Max nb = 1026
(click on the image to enlarge it)
 

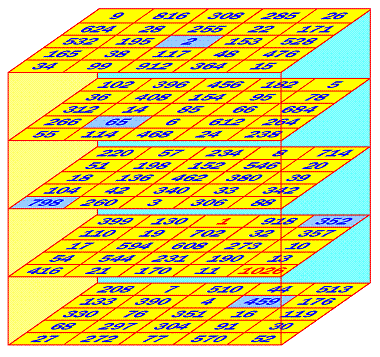
All its rows, columns, pillars and 4 triagonals are magic. And this cube has a very nice additional property: all its broken triagonals are magic, as the example in blue.

In May 2010, Toshihiro Shirakawa constructed a 5th-order multiplicative magic cube with smaller characteristics than my above cube: P = 13,967,553,600 and MaxNb = 855. Also with magic broken triagonals. This is today the best known 5th-order magic cube! You can see it in the downloadable Excel file, below the table. Similarly to his 4th-order method, he used my 5th-order multiplicative magic square (reproduced below), combined with (1, 11, 13, 17, 19). My above cube was an Eulerian cube (1, 2, 3, 4, 6) (1, 5, 7, 8, 9) (1, 11, 13, 17, 19).

Unfortunately the plane diagonals of our two cubes are not magic: they are not perfect magic cubes. However, it is possible to construct 5th-order perfect magic cubes: use the first known 5th-order (additive) perfect magic cube constructed by Walter Trump and me in 2003, and replace each number n by 2^(n-1). Then you will get a multiplicative perfect magic cube... but tedious... using very big numbers: Max nb = 2^(125-1) = 2.13 · 10^37, and P = 2^310 = 2.09 · 10^93. In December 2012, Toshihiro Shirakawa constructed two far better 5th-order perfect magic cubes: one with Max nb = 250 880, one with P = 2520^5 = 1.01 · 10^17. Astonishingly, but with a larger order, perfect cubes using smaller integers are known: see my 11th-order pandiagonal perfect cube with Max nb = 24 992 < 250 880.

6th-order multiplicative magic cubes

In January 2006, I constructed two cubes:

These cubes are only semi-magic: their 4 triagonals are not magic.

Later, in May 2006, I constructed a magic cube, this time with 4 magic triagonals. This added feature has a cost, bigger P and Max nb than the previous semi-magic cubes:

Then in June 2010, Toshihiro Shirakawa constructed a magic cube with much smaller characteristics than my poor above cube:

This is today the best known 6th-order magic cube!

It is possible to construct 6th-order perfect magic cubes: use the first known 6th-order (additive) perfect magic cube constructed by Walter Trump in 2003, and replace each number n by 2^(n-1). Then you will get a multiplicative perfect magic cube... but tedious... using very big numbers: Max nb = 2^(216-1) = 5.27 · 10^64, and P = 2^645 = 1.46 · 10^194. In December 2012 and February 2013, Toshihiro Shirakawa constructed two far better 6th-order perfect magic cubes: one with Max nb = 66 924, one with P = 2 882 880^3 = 2.39 · 10^19. Astonishingly, but with a larger order, perfect cubes using smaller integers are known: see my 11th-order pandiagonal perfect cube with Max nb = 24 992 < 66 924.

7th-order multiplicative magic cubes

In January 2006, my two best magic cubes were:

But in May 2010, Toshihiro Shirakawa constructed better cubes:

As the above 5th-order magic cubes, all their broken triagonals and 4 entire triagonals are magic, but their plane diagonals are not magic: they are not perfect magic cubes. With the same P and Max nbs, I have successfully constructed cubes with all their magic plane diagonals... but unfortunately loosing 2 magic triagonals on the 4 triagonals.

Keeping magic plane diagonals, I have constructed -still in January 2006- two cubes with 3 magic triagonals (now, only one triagonal is bad!) with the cost of using bigger characteristics:

and finally succeeded in constructing perfect magic cubes with 4 magic triagonals, but with again bigger characteristics. To get the 4th triagonal is very expensive!

8th to 11th-order multiplicative magic cubes

See the summary in the table at the beginning of this page. And see the page on the pandiagonal perfect multiplicative magic cubes.

To celebrate January 2006 when the cubes were created, the two first numbers used in my 10th and 11th-order cubes are: "2006" and "1"!

Return to the home page http://www.multimagie.com