List of the site's news added November 6, 2007
- Death on July 7th 2007 of John R. Hendricks,
Canada, the magic "tesseracts" master.
I had been pleased to have
dedicated to him in
2003 my multimagic
hypercubes, the first known multimagic "tesseracts".
- Two impressive results after a joint work of Jaroslaw Wroblewski,
Poland, and Hugo Pfoertner, Germany:
 "Better late than never".
"Better late than never".
In The American Mathematical
Monthly, October 2007, my SOLUTION OF A PROBLEM PROPOSED 66
YEARS AGO in this same magazine (problem E 496 published in 1941 by Royal
Vale Heath, USA)- Coincidence: in this same issue of The American Mathematical
Monthly, paper "Multimagic squares" by Harm Derksen, Christian Eggermont,
and Arno van den Essen, USA/Netherlands. See
the page on Highly multimagic squares
where this interesting paper -draft initially written in 2005- was already
presented here since January 2006 : some criticism on their paper is
added.
- And again in the same issue of the Monthly, bimagic
square of order 13 by Chen Qinwu,
China, already
presented here since April 2006
- New best known
pandiagonal multiplicative magic squares of orders 8, 9, and 10,
12, 14 constructed by a joint work of Jaroslaw Wroblewski, Poland,
and me.
Look also at the updated records table.
- New page on the smallest additive-multiplicative
magic square problem: orders 5, 6, and 7 are unknown!
Add-mult semi-magic squares
of orders 4, 5, 6 by Lee Morgenstern, USA,
including this nice add-mult nearly magic square of order 5:
|
105
|
182
|
40
|
198
|
45
|
|
78
|
216
|
66
|
175
|
35
|
|
220
|
42
|
65
|
63
|
180
|
|
140
|
55
|
189
|
30
|
156
|
|
27
|
75
|
210
|
104
|
154
|
- Thanks to Noel Flower, New Zealand,
to have reported errors on the children of Andrew Frost
(1819-1907). His biography is now corrected.

 The Mathematical Intelligencer, Vol. 29,
N.1 and N.2, 2007.
The Mathematical Intelligencer, Vol. 29,
N.1 and N.2, 2007.
My paper "Sudoku's French Ancestors"
is published in two parts. It is the English version of my paper previously
published in Pour La Science in 2006. Thanks to Chandler Davis,
Canada, Michael Kleber and Ravi Vakil, USA.
- ??!!??
REMINDER of some of the most wanted
problems on "small" objects, extracted from the updated Problems
page.
Is it possible to construct, using distinct integers:
- a 3x3 magic square of
squares?
- a 4x4 magic
square of cubes? or 5x5, 6x6, 7x7, 8x8? (using distinct positive integers)
- a 5x5 bimagic square?
- a 5x5 additive-multiplicative magic square? or 6x6, 7x7? (new page
on this problem, as said above)
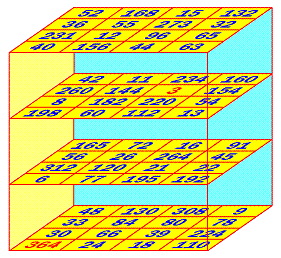
- a ?x?x? multiplicative magic cube using distinct integers < 364?
(new progress mentioned above: it was still 416 in my previous update)
Return to the home page http://www.multimagie.com