Séries multimagiques pour cubes
Voir aussi
les séries multimagiques pour carrés
Comme nous l'avons vu pour le plus petit cube bimagique, il peut être intéressant,
pour essayer de construire un cube p-multimagique d'ordre n, de trouver l'ensemble
des séries p-multimagiques d'ordre n, c'est-à-dire des
séries de n entiers différents compris entre 1 et n3, ayant la bonne
somme magique, bimagique,... jusqu'à p-multimagique (= S1, S2,... Sp):
- S1 = n(n3 + 1)/2
- S2 = n(2n6 + 3n3 + 1)/6
- S3 = n(n9 + 2n6 + n3)/4 = n2 S12
- S4 = n(6n12 + 15n9 + 10n6 - 1)/30
- S5 = (3n2S22 - S3)/2
L'ordre 3 permet d'obtenir des séries bimagiques.
Voici les 4 séries bimagiques possibles :
- 3 19 20
- 4 15 23
- 5 13 24
- 8 9 25
Cela signifie donc que :
- 3 + 19 + 20 = 4 + 15 + 23 = 5 + 13 + 24 = 8 + 9 + 25 = 42 = S1
- 3² + 19² + 20² = 4² + 15² + 23² = 5² + 13² + 24² = 8² + 9² + 25² = 770
= S2
Pour l'ordre 4, il y a 8 séries bimagiques dont la liste est
donnée dans la page du Plus petit cube bimagique.
Voici un tableau récapitulatif du nombre de séries magiques, certaines listes
étant
téléchargeables sous la forme de fichiers Excel, entre 44Ko et 540Ko chacun.
Les nombres des séries bimagiques d'ordre 9 et 10 ont été calculées par Walter
Trump, Allemagne, en octobre 2005. Le nombre des séries trimagiques d'ordre
9 a été calculé par Gildas Guillemot, France, en décembre 2006 ensuite
confirmé par Michael Quist, USA, en mai 2008. Les nombres des séries bimagiques d'ordre
11 et 12 ont été calculés en mai et juin 2013 par Walter Trump, en utilisant
un programme écrit par Lee Morgenstern, USA. En août 2015, Dirk
Kinnaes, Belgique, a confirmé les nombres précédemment connus de séries
bimagiques, et a calculé le nombre de séries bimagiques d'ordre 13 : voir son
algorithme (fichier PDF
en anglais).
Number of multimagic series for cubes
|
Ordre
|
Bimagique
|
Trimagique
|
Tétramagique
|
Pentamagique
|
Hexamagique
|
|
3
|
4
|
0
|
0
|
0
|
0
|
|
4
|
8
|
0
|
0
|
0
|
0
|
|
5
|
272
|
0
|
0
|
0
|
0
|
|
6
|
25270
|
(a)
0
|
0
|
0
|
0
|
|
7
|
5152529
|
161
|
0
|
0
|
0
|
|
8
|
1594825624
|
17218
|
0
|
0
|
0
|
|
9
|
651151145259 |
363949
|
(b)
0
|
0
|
0
|
|
10
|
347171191981324 |
(a)
0
|
0
|
0
|
0
|
|
11
|
315035719463520007
|
Inconnu ! (d) (f) > 5.4
· 109
|
(e) 0
|
0
|
0
|
|
12
|
333498789992790704850
|
Inconnu ! (d) (f) >
2.5 · 1012
|
(e) 0
|
0
|
0
|
|
13
|
450285458654002877929960
|
Inconnu ! (d) (f) >
1.6 · 1015
|
Inconnu ! (d)
|
(e) 0
|
0
|
|
14
|
Inconnu ! (c) ~ 7,4 · 1026
|
(a)
0
|
0
|
0
|
0
|
|
15
|
Inconnu ! (c) ~ 1,5 · 1030
|
Inconnu ! (d) (f) >
1.4 · 1021
|
Inconnu !!!!!!
|
(e) 0
|
0
|
|
16
|
Inconnu ! (c) ~ 3,7 · 1033
|
Inconnu ! (d) (f) >
1.9 · 1024
|
Inconnu ! (d)
|
Inconnu ! (d)
|
(e) 0
|
|
17
|
Inconnu ! (c) ~ 1,1 · 1037
|
Inconnu ! (d) (f) >
3.0 · 1027
|
(e) 0
|
0
|
0
|
|
18
|
Inconnu ! (c) ~ 3,7 · 1040
|
(a)
0
|
0
|
0
|
0
|
(a) Les séries trimagiques d'ordre 4k+2 sont impossibles
: il est impossible d'avoir S3 pair avec S1 impair et S2
impair.
(b) Courte et belle preuve de Robert Gerbicz, Hongrie,
en janvier 2006. "Pour l'ordre 9, la somme tétramagique est S4=510.118.152.189==13 mod 16.
Mais (2*x+1)^4==1 mod 16 et (2*x)^4==0 mod 16 : cela signifie qu'au moins 13 nombres
impairs sont nécessaires. Impossible avec seulement 9 nombres !"
(c) Estimations des
séries bimagiques par Michael Quist, juin 2013.
(d) Nombres inconnus
de séries, mais séries existantes, exemples
trouvés par Lee Morgenstern, avril-mai 2015
(e) Preuves
d'impossibilité par Lee Morgenstern, avril-mai 2015
(f) Estimations des
séries trimagiques par Dirk Kinnaes,
mars 2017
En juin 2013, Michael Quist a écrit un
article estimant les nombres des séries magiques et multimagiques, dont les
séries bimagiques pour cubes d'ordre N. Voir http://arxiv.org/abs/1306.0616.
Voici sa formule, et les valeurs numériques obtenues pour 10 ≤ N ≤ 18.
L'erreur décroit avec les plus grands ordres. En août 2015, Dirk Kinnaes
a amélioré la formule de Quist, en ajoutant un nouveau terme (voir aussi son fichier
PDF donné plus haut).
Nombres estimés de séries bimagiques, formule de Michael
Quist :
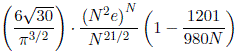
Améliorée
en ajoutant le terme + 16333813 / 7847840N², par Dirk
Kinnaes.
Comparaison
avec les nombres exacts.
Ordre | Quist
nombre
estimé | Kinnaes
nombre
estimé | Nombre
exact | Quist
erreur | Kinnaes
erreur |
10 | 3,607 · 1014 | 3,693 · 1014 | 347171191981324 | +3,90% | +6,36% |
11 | 2,971 · 1017 |
3,029 · 1017 |
315035719463520007
| -5,68% | -3,86% |
12 | 3,197 · 1020 |
3,248 · 1020 |
333498789992790704850
| -4,15% | -2,61% |
13 | 4,365 · 1023 | 4,424 · 1023 |
450285458654002877929960
| -3,07% | -1,75% |
14 | 7,389 · 1026 | 7,475 · 1026 | ? | ? |
|
15 | 1,521 · 1030 | 1,536 · 1030 | ? | ? |
|
16 | 3,747 · 1033 | 3,780 · 1033 | ? | ? |
|
17 | 1,089 · 1037 | 1,098 · 1037 | ? | ? |
|
18 | 3,691 · 1040 | 3,716 · 1040 | ? | ? |
|
En mars 2017, Dirk Kinnaes a écrit
un article "Estimating the number of K-multimagic hypercube series"
(fichier PDF en anglais) incluant
une formule estimant les nombres de séries trimagiques pour cubes d'ordre N.
Voici sa formule, et les valeurs numériques obtenues pour 7 ≤ N ≤ 15. L'erreur décroîtra avec les plus grands ordres,
on devrait espérer de bien plus petites erreurs pour les ordres > 10.
Nombres estimés de séries trimagiques,
formule
de Dirk Kinnaes :
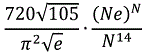
Comparaison
avec les nombres exacts.
Ordre | Kinnaes
nombre
estimé | Nombre
exact | Kinnaes
erreur |
7 | 7.0 | 161 | / 23.1 |
8 |
544.0 |
17218
| / 31.6 |
9 |
74781.2 |
363949
| / 4.9 |
10 | 1.65 · 107 |
0
| --- |
11 | 5.42 · 109 | ? |
?
|
12 | 2.52 · 1012 | ? |
?
|
13 | 1.60 · 1015 | ? |
?
|
14 | 1.33 · 1018 | 0 |
---
|
15 | 1.41 · 1021 | ? |
?
|
Les séries bimagiques et trimagiques sont référencées respectivement sous
les numéros A090653 et A092312
dans la On-Line Encyclopedia
of Integer Sequences, OEIS Foundation.
Retour à la page d'accueil http://www.multimagie.com