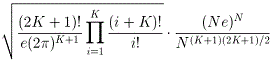Séries multimagiques pour carrés
Voir aussi
les séries multimagiques pour cubes
Comme nous l'avons vu pour le plus petit carré bimagique et
le plus petit carré trimagique, il peut être intéressant,
pour essayer de construire un carré p-multimagique de taille nxn, de trouver l'ensemble
des séries p-multimagiques d'ordre n, c'est-à-dire des
séries de n entiers différents compris entre 1 et n², ayant la bonne
somme magique, bimagique,... jusqu'à p-multimagique.
L'ordre 4 est le plus petit ordre permettant d'obtenir des séries bimagiques.
Voici ces 2 séries bimagiques, qui sont aussi étonnamment trimagiques :
Cela signifie donc que :
- 15 + 9 + 8 + 2 = 14 + 12 + 5 + 3 = 34 = S1
- 152 + 92 + 82 + 22 = 142 + 122 + 52 + 32 = 374 = S2
- 153 + 93 + 83 + 23 = 143 + 123 + 53 + 33 = 4624 = S3
Pour l'ordre 5, il y a 8 séries bimagiques dont la liste est
donnée dans la page du Plus petit carré bimagique.
Voici un tableau récapitulatif du nombre de séries magiques. Certaines listes
sont
téléchargeables sous la forme de fichiers Excel, entre 28Ko et 800Ko chacun.
Pour l'ordre 12, les nombres des séries trimagiques, tétramagiques et pentamagiques
ont été sympathiquement
communiqués par Walter Trump,
Allemagne. En 2004, les nombres de Walter Trump ont été confirmés par Fredrik
Jansson, Finlande. Et Fredrik est allé plus loin : il est le premier à avoir calculé
le gros nombre de séries bimagiques d'ordre 12, et le nombre de séries multimagiques
d'ordre 13 (sauf les séries bimagiques d'ordre 13).
Nouveaux résultats sur les séries bimagiques, entre juillet et octobre
2005, en provenance d'Allemagne :
- Grâce à une nouvelle méthode, Lorenz Schlangen est le premier
à calculer les nombres de séries d'ordres 13, 14 et 15
- Walter confirme, quelques semaines après Lorenz, et avec la nouvelle
méthode de Lorenz (mais un programme différent) les trois nombres
- Et Walter va encore plus loin : avec la même nouvelle méthode, il est
le premier à calculer les nombres des séries bimagiques d'ordres 16 et 17
En avril 2008, Michael Quist, USA, a calculé les nombres de séries tétramagiques
et pentamagiques d'ordre 16. En mai 2008, il a calculé le nombre de séries
trimagiques d'ordre 15 (et a aussi confirmé le nombre de séries trimagiques
d'ordre 13 précédemment calculé par Fredrik Jansson). En août 2008, il
a calculé le nombre de séries bimagiques des ordres 18, 19 et 20 (et a
aussi confirmé le nombre de séries bimagiques des ordres inférieurs déjà calculés).
En mai 2013,
il
a calculé le nombre de séries bimagiques des ordres 21, 22, 23, nombres indépendemment
calculés et confirmés quelques jours plus tard par Lee Morgenstern, USA. Puis
en mai et juin 2013, en utilisant directement le logiciel écrit par Lee Morgenstern
(PDF avec méthode
de comptage de L. Morgenstern, en anglais), Walter Trump a calculé le nombre de séries bimagiques des ordres 24, 25, 26, 27 et 28. En
décembre
2014, Lee Morgenstern a calculé le nombre de séries trimagiques des ordres 16
et 17. En août 2015, Dirk Kinnaes, Belgique, a confirmé les nombres
précédemment connus de séries bimagiques, et a calculé les nombres de séries
bimagiques des ordres 29 et 30 (PDF
avec algorithme de Kinnaes, en anglais).
Nombre de séries multimagiques pour carrés
(cliquer dans
les cellules pour télécharger les fichiers Excel correspondants)
|
Ordre
|
Bimagique
|
Trimagique
|
Tétramagique
|
Pentamagique
|
Hexamagique
|
|
3
|
0
|
0
|
0
|
0
|
0
|
|
4
|
2
|
2
|
0
|
0
|
0
|
|
5
|
8
|
2
|
0
|
0
|
0
|
|
6
|
98
|
(a)
0
|
0
|
0
|
0
|
|
7
|
1844
|
0
|
0
|
0
|
0
|
|
8
|
38039
|
121
|
0
|
0
|
0
|
|
9
|
949738
|
126
|
0
|
0
|
0
|
|
10
|
24643236
|
(a)
0
|
0
|
0
|
0
|
|
11
|
947689757
|
31187
|
0
|
0
|
0
|
|
12
|
45828982764
|
2226896
|
106
|
4
|
0
|
|
13
|
2151748695931
|
17265701
|
555
|
3
|
0
|
|
14
|
123821075526032 |
(a)
0
|
0
|
0
|
0
|
|
15
|
8131094055190149 |
69303997733 |
(b)(c)
0
|
0
|
0
|
|
16
|
573957471153552576
|
1683487116508
|
235275
|
13
|
0
|
|
17
|
44010987379157415768
|
112205432382966
|
(c) 0
|
0
|
(f)(g) 0
|
|
18
|
3655486139293429450720 |
(a)
0
|
0
|
0
|
0
|
|
19
|
333633403912637510806972 |
Inconnu ! (h) ~ 2.00 · 1017
|
Inconnu ! (d) > 0
|
(e) 0
|
(f)(g) 0
|
|
20
|
32862657239386515532593520
|
Inconnu ! (h) ~ 1.41 · 1019
|
Inconnu ! (d) > 0
|
Inconnu ! (d) > 0
|
(g) 0
|
|
21
|
3431453899306300581868236386
|
Inconnu ! (h) ~ 1.08 · 1021
|
Inconnu ! (d) > 0
|
Inconnu ! (d) > 0
|
(g) 0
|
|
22
|
384125946998166710305616659402
|
(a)
0
|
0
|
0
|
0
|
|
23
|
45801639842337348432002857205878
|
Inconnu ! (h) ~ 7.96 · 1024
|
Inconnu ! (d) > 0
|
(e) 0
|
(g) 0
|
|
24
|
5773407884408951768360741341457291
|
Inconnu ! (h) ~ 7.61 · 1026
|
Inconnu ! (d) > 0
|
Inconnu ! (d) > 0
|
(g) 0
|
|
25
|
768467875608077797720790265285636797
|
Inconnu ! (h) ~ 7.78 · 1028
|
Inconnu ! (d) > 0
|
(e) 0
|
(g) 0
|
|
26
|
107710220763567919574782844625088827344
|
(a)
0
|
0
|
0
|
0
|
|
27
|
15880475347526962316266889239839811859979
|
Inconnu ! (h) ~ 9.78 · 1032
|
Inconnu ! (i) > 0
|
Inconnu ! (i) > 0
|
Inconnu !!!!!!
|
|
28
|
2455456581123976779162274548131606029110869
|
Inconnu ! (h) ~ 1.19 · 1035
|
Inconnu ! (d) > 0
|
Inconnu ! (d) > 0
|
(g) 0
|
|
29
|
397017067970073855910942668942599683652058914
|
Inconnu ! (h) ~ 1.54 · 1037
|
Inconnu ! (d) > 0
|
Inconnu ! (d) > 0
|
(g) 0
|
|
30
|
67063309991205148544594890672812817873237628826
|
(a)
0
|
0
|
0
|
0
|
|
31
|
Inconnu ! (h) ~ 1.181 · 1049
|
Inconnu ! (h) ~ 2.97 · 1041
|
Inconnu !!!!!!
|
(j) 0
|
(g) 0
|
|
32
|
Inconnu ! (h) ~ 2.165 · 1051
|
Inconnu ! (h) ~ 4.43 · 1043
|
Inconnu ! (d) > 0
|
Inconnu ! (d) > 0
|
(g) 0
|
(a) Les séries trimagiques d'ordre 4k+2 sont impossibles
: il est impossible d'avoir S3 pair, avec S1 impair et S2
impair.
(b) Les séries tétramagiques d'ordre 15 sont impossibles : voir
plus bas la preuve de Robert Gerbicz, Hongrie,
en 2006.
(c) Les séries tétramagiques des ordres 15 et 17 sont impossibles : voir
plus bas les preuves de
Lee Morgenstern, USA, en 2013
(d) Ces séries tétramagiques et
pentamagiques sont difficiles à trouver, mais sont possibles : voir plus
bas les exemples de Lee Morgenstern, en 2013
(e) Les séries pentamagiques
des ordres 19 et 23 sont impossibles : voir plus bas les preuves
de Lee Morgenstern, en 2013
(f) Les séries hexamagiques des ordres 17 et 19
sont impossibles : voir plus bas les preuves
de Jaroslaw Wroblewski, Pologne, en 2008.
(g)
Les séries hexamagiques des ordres de 12 à 39 (sauf l'ordre inconnu
27) sont impossibles : voir plus bas les preuves de Lee Morgenstern, en
2013.
(h) Estimations
des séries bimagiques et trimagiques, voir plus pas les formules de Michael Quist,
2013.
(i) Les séries pentamagiques d'ordre 27 sont possibles :
voir plus bas les exemples de Christian Boyer
et Lee Morgenstern, en 2013.
(j) Les séries pentamagiques d'ordre
31 sont impossibles: voir plus bas la preuve
de Jean Moreau de Saint-Martin, en 2013.
L'ordre 12 est donc le plus petit ordre permettant d'obtenir des séries tétra
et pentamagiques. Sur les 106 séries tétramagiques, 4 sont de plus pentamagiques. Elles sont toutes symétriques
gauche/droite, c'est-à-dire i-ème nombre + (13-i)ème nombre = 12² + 1 = 145.
- 143 116 109 108 100 85 60 45 37 36 29 2
- 140 124 117 97 90 89 56 55 48 28 21 5
- 137 127 121 100 81 80 65 64 45 24 18 8
- 135 129 123 95 86 78 67 59 50 22 16 10
Quel est le plus petit ordre permettant d'obtenir des séries hexamagiques
? Les plus petits candidats actuels sont les ordres 27 et 40.
Les séries bimagiques, trimagiques, tétramagiques et pentamagiques sont référencées respectivement sous
les numéros A052457, A052458, A090037
et A106646
dans la On-Line Encyclopedia
of Integer Sequences, OEIS Foundation.
Voir aussi le sujet
"Multimagic Series" dans le World
of Mathematics d'Eric Weisstein, Wolfram Research.
En avril-mai 2005, Walter Trump calculait une estimation du
nombre de séries magiques variées, dont les séries bimagiques d'ordre 13 à 20,
en utilisant des méthodes Monte Carlo. Plus de détails à www.trump.de/magic-squares/magic-series/index.html.
Les nombres exacts de séries bimagiques, calculés après son estimation
(voir plus haut), sont très proches : sa méthode d'estimation est prouvée excellente
!
Nombres de séries bimagiques, estimées par Walter Trump. Comparaison
avec les nombres exacts.
|
Ordre
|
Nombre estimé
|
Nombre exact
|
Erreur
|
|
13
|
2,16 · 1012
|
2151748695931
|
0,38%
|
|
14
|
1,24 · 1014
|
123821075526032 |
0,14%
|
|
15
|
8,15 · 1015
|
8131094055190149 |
0,23%
|
|
16
|
5,74 · 1017
|
573957471153552576
|
0,01%
|
|
17
|
4,41 · 1019 |
44010987379157415768
|
0,20%
|
|
18
|
3,65 · 1021 |
3655486139293429450720 |
0,15%
|
|
19
|
3,33 · 1023 |
333633403912637510806972 |
0,19%
|
|
20
|
3,29 · 1025 |
32862657239386515532593520
|
0,11%
|
En juin 2013, Michael Quist a écrit un
article estimant les nombres des séries magiques et multimagiques, incluant
les séries bimagiques pour carrés d'ordre N. Voir http://arxiv.org/abs/1306.0616.
Voici sa formule, et les valeurs numériques obtenues pour 20 ≤ N ≤ 32. L'erreur
décroit avec les plus grands ordres. En août 2015, Dirk Kinnaes a amélioré
la formule de Quist, en ajoutant un nouveau terme (voir aussi son fichier
PDF donné plus haut).
Nombres estimés de séries bimagiques, formule
de Michael
Quist:
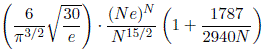
Améliorée
en ajoutant le terme + 11522051 / 70630560N², par Dirk
Kinnaes.
Comparaison
avec les nombres exacts.
Ordre | Quist
nombre
estimé | Kinnaes
nombre
estimé | Nombre
exact | Quist
erreur | Kinnaes
erreur |
20 | 3.27798 · 1025 | 3.27668 · 1025 | 32862657239386515532593520
| -0.2521% | -0.2916% |
21 | 3.43856 · 1027 |
3.43732 · 1027 |
3431453899306300581868236386
| +0.2070% | +0.1710% |
... | ... |
... |
... |
... |
... |
27 | 1.58874 · 1040 |
1.58839 · 1040 |
15880475347526962316266889239839811859979
|
+0.0436%
|
+0.0217%
|
28 | 2.45557 · 1042 |
2.45507 · 1042 |
2455456581123976779162274548131606029110869
|
+0.0045%
|
-0.0159%
|
29 | 3.97141 · 1044 |
3.97066 · 1044 |
397017067970073855910942668942599683652058914
|
+0.0313%
|
+0.0123%
|
30 | 6.70832 · 1046 |
6.70713 · 1046 |
67063309991205148544594890672812817873237628826
|
+0.0296%
|
+0.0119%
|
31 | 1.18141 · 1049 |
1.18122 · 1049 |
?
|
?
|
?
|
32 | 2.16576 · 1051 |
2.16542 · 1051 |
?
|
?
|
?
|
Ce n'est pas dans son article, mais Michael Quist a calculé en mai 2013 cette
autre formule :
Les nombres estimés par cette formule, pour N > 18, sont dans la colonne
trimagique de la
première table de cette page.
Et en décembre 2013, il a proposé cette
formule générale pour les séries multimagiques d'ordre N (la précédente formule
trimagique en découle avec K=3) :
En janvier 2006, Robert Gerbicz, Hongrie, a prouvé
qu'il n'y a pas de série tétramagique d'ordre 15. Voici sa preuve.
Les sommes magiques sont :
- S1=1695
- S2=254815
- S3=43095375
- S4=7774354687
S4==15
mod 16. Puisque (2x+1)^4==1 mod 16 et (2x)^4==0
mod 16, les 15 nombres doivent être impairs.
Soit a(k)=2b(k)+1 (où chaque b(k) est un entier) et
T1=somme(b(k), k=1..15), T2=somme(b(k)^2, k=1..15), et ainsi de suite...
Par le théorème du binôme, on a :
- S1=somme(2b(k)+1, k=1..15) = 2*T1+15 = 1695
- S2=somme((2b(k)+1)^2, k=1..15) = 4*T2+4*T1+15 = 254815
- S3=somme((2b(k)+1)^3, k=1..15) = 8*T3+12*T2+6*T1+15 = 43095375
- S4=somme((2b(k)+1)^4, k=1..15) = 16*T4+32*T3+24*T2+8*T1+15 = 7774354687
Il est facile de résoudre ce système linéaire d'équations :
- T1=840
- T2=62860
- T3=5292000
- T4=475218457
Il y a une contradiction. Puisque x==x^4 mod
2, il devrait y avoir T1==T4 mod 2 : mais T1 est pair et T4 est impair !
Il n'y a donc pas de série tétramagique (et pentamagique, hexamagique...) pour
carrés d'ordre 15.
En juillet 2008, Jaroslaw Wroblewski, Pologne, a
prouvé qu'il n'y a pas de série hexamagique d'ordre 17. Voici sa preuve.
A partir de S4=1(mod 17) on conclut que les
séries doivent contenir 17 termes impairs, ou un terme impair et 16 termes pairs.
***** Dans le cas de 17 termes impairs, chacun
de la
forme 4k+1 (où k peut être négatif)(*), en notant Ki la somme des puissances i
des k, on obtient
- S2 = 475745 = 16 K2 + 4 K1 + 17
- S4 = 23923217921 = 256 K4 + 256 K3 + 96
K2 + 16 K1 + 17
soit encore
- 59466 = K1 + 2 K2
- 1495201119 = K1 + 6 K2 + 16 K3 + 16 K4
ce qui donne une contradiction sur la parité
de K1. Il n'y a donc pas de série tétramagique dans ce cas.
***** Dans le cas de 1 terme impair de la forme 4k+1
(où k peut être négatif) et 16 termes pairs de la forme 2p, en notant
Pi la somme des puissances i des p, on obtient à partir des équations de S2
et S4, respectivement:
- 118936 = 2 k + 4 k^2 + P2
- 1495201120 = k + 6 k^2 + 16 k^3 + 16 k^4
+ P4
Comme P2 et P4 ont la même parité, k doit être
impair, notons k = 2m. On obtient à partir de l'équation sur S6 :
- 89508435052624 = 3 m + termes_divisibles_par_4
ce qui nous permet d'écrire m=4r. On obtient
à partir des équations de S2 et S6 :
- 118936 = P2 + 16 r + 256 r^2
- 22377108763156 = P6 + 3 r + termes_divisibles_par_8
Puisque P2=P6(mod 4), on peut noter r=4q. Maintenant
le terme impair de la série magique est égal à 128q+1, q = -2,-1,0,1,2.
A partir de l'équation sur S4, qui prend
cette forme
- 1495201120 = P4 + 32 q + 6144 q^2 + 524288
q^3 + 16777216 q^4
on conclut que P4 est divisible par 32 et puisque P4 = P6 (mod 8), P6 est divisible par 8.
L'équation sur S6 donne :
- 22377108763156 = P6 + 12 q + termes_divisibles_par_8
Cela force q à être impair, c'est-à-dire q doit
valoir plus ou moins 1.
Dans le cas q=1 on obtient :
- P2 = 114776
- P4 = 1477893440
- P6 = 22305104487176
Dans le cas q=-1 on obtient :
- P2 = 114904
- P4 = 1478942080
- P6 = 22311548248864
Dans chaque cas P4 est divisible par 16, ce
qui signifie que tous les p sont impairs ou que tous sont pairs. Toutefois P6 n'est
pas divisible par 64,
ce qui exclut la possibilité de tous les p impairs. Notons p=4x+1 (x étant
un entier de tout signe).
A partir des équations sur S2 et S4 on obtient
pour
q=1:
- 14345 = X1 + 2 X2
- 92368339 = X1 + 6 X2 + 16 X3 + 16 X4
et pour q=-1:
- 14361 = X1 + 2 X2
- 92433879 = X1 + 6 X2 + 16 X3 + 16 X4
Dans chacun des cas il y a une contradiction
mod 4.
Et toujours en juillet 2008, Jaroslaw Wroblewski a prouvé qu'il n'y
a pas de série hexamagique d'ordre 19. Voici sa preuve.
S4(mod 16)=7, implique que toute série doit
avoir 7 termes impairs et 17 pairs, de la forme 4k+1 et 2p respectivement. Alors
les équations sur S2, S4, S6 donnent :
- 207198 = 2 K1 + 4 K2 + P2
- 4061581299 = K1 + 6 K2 + 16 K3 +
16 K4 + P4
- 758246942365254 = 3 K1 + 30 K2 +
160 K3 + 480 K4 + 768 K5 + 512 K6 + 8 P6
La dernière équation indique un K1 pair, et
donc P2 et
P4 ont une contradiction de parité, ce qui prouve qu'il n'y a pas de série hexamagique d'ordre
19.
(*) Au sujet des termes impairs de la forme 4k+1 "où k
peut être négatif". Oui, chaque entier impair, ou son opposé, est bien
de la forme 4k+1 :
- 1 = 4*0+1
- -3 = 4*(-1)+1
- 5 = 4*1+1
- -7 = 4*(-2)+1
- 9 = 4*2+1
- -11 = 4*(-3)+1
etc, avec k = 0, -1, 1, -2, 2, -3,... Jolie astuce!
De mars à août 2013, Lee Morgenstern
a prouvé qu'il n'y a pas de séries tétramagiques des ordres 3, 4, 5, 7, 8, 9,
11, 15 et 17. A prouvé qu'il n'y a pas de séries pentamagiques des ordres
19, 23 et 25. Et a prouvé qu'il n'y a pas de séries hexamagiques des ordres
12, 13, 16, 19, 20, 21, 23, 24, 25, 28, 29, 31, 32, 33, 35, 36, 37 et 39.
Les existences des séries hexamagiques des ordres 27 et 40 (et de nombreux >40) sont
inconnues.
En juillet et août 2013, il a prouvé que quelques séries multimagiques existent, en
trouvant des exemples :
- Tétramagique 19, avec (316, 315,
314, 313, 311, 309, 230, 206, 173, 146, 142, 131, 126, 116, 110, 107, 64,
8, 2)
- Pentamagique 20, avec (400, 383, 311, 302, 294, 287,
281, 276, 274, 263, 138, 127, 125, 120, 114, 107, 99, 90, 18, 1)
- Pentamagique 21, avec (437, 429, 346, 336,
332, 331, 321, 302, 298, 288, 221, 154, 144, 140, 121, 111, 110, 106, 96,
13, 5)
- Tétramagique 23, avec (514, 499, 459, 454,
439, 427, 379, 319, 314, 307, 283, 274, 259, 223, 211, 199, 139, 124, 94,
64, 49, 34, 31)
- Pentamagique 24, avec (576, 569, 467, 453, 435, 425,
414, 411, 404, 397, 394, 355, 222, 183, 180, 173, 166, 163, 152, 142, 124,
110, 8, 1)
- Tétramagique 25, avec (559, 558, 556, 554, 551,
544, 524, 433, 409, 341, 337, 313, 304, 277, 253, 229, 217, 196, 181, 157,
153, 109, 49, 12, 9)
En octobre 2013, Christian Boyer a trouvé cette famille
symétrique :
- Pentamagique 27, avec (35, 42, 45, 99, 105,
a, 190, b,
245, 275, 289, c, 361,
365, 369, 730-c, 441,
455, 485, 730-b, 540,
730-a, 625, 631, 685,
688, 695)
- (a,
b, c)
= (133, 203, 295), ou (135, 197, 303), ou (155, 163, 357).
et de Lee Morgenstern :
- Pentamagique 27, avec (729, 720, 605, 601, 575,
573, 553, 549, 545, 505, 473, 430, 405, 365, 325, 300, 257, 225, 185, 181,
177, 157, 155, 129, 125, 10, 1)
- Pentamagique 28, avec (710, 709, 708, 707, 706,
704, 679, 523, 476, 471, 466, 444, 426, 423, 362, 359, 341, 319, 314, 309,
262, 106, 81, 79, 78, 77, 76, 75)
- Pentamagique 29, avec (799, 798, 797, 795, 658,
628, 622, 604, 592, 578, 574, 570, 547, 430, 421, 412, 295, 272, 268, 264,
250, 238, 220, 214, 184, 47, 45, 44, 43)
- Pentamagique 32, avec (931, 930, 929, 928,
927, 926, 924, 826, 697, 643, 628, 612, 607, 598, 552, 517, 508, 473, 427,
418, 413, 397, 382, 328, 199, 101, 99, 98, 97, 96, 95, 94)
- Pentamagique 40, avec (1431, 1430, 1429, 1428,
1427, 1426, 1424, 1423, 1421, 1420, 1374, 891, 867, 864, 860, 859, 838, 828, 825, 804,
797, 776, 773, 763, 742, 741, 737, 734, 710, 227,
181, 180, 178, 177, 175, 174, 173, 172, 171, 170)
En septembre-octobre 2013, Jean Moreau de Saint-Martin,
France, a étudié et vérifié en détails les preuves de Morgenstern sur les séries
multimagiques (à partir des fichiers texte zippés ci-dessus), et n'a pas trouvé
d'erreur.
Et il a été plus loin, simplifiant et généralisant les preuves de Morgenstern.
Aussi utilisant quelques-unes de mes remarques et calculs, nous avons maintenant de nouvelles
preuves d'impossibilité :
- Les séries pentamagiques d'ordre 31 sont impossibles
- Les séries hexamagiques des ordres 43, 44, 47, 48, 49, 52, 60, 63, 65 sont impossibles
Voilà cette étude sur les séries multimagiques :
En février 2017, Lee Morgenstern a récapitulé ses
nombreuses preuves
sur les séries multimagiques (en anglais) jusqu'à l'ordre 44, et jusqu'aux octamagiques.
Sa remarque :
"Importantes sont les preuves mathématiques
des trimagiques d'ordre 7 et des hexamagiques d'ordre 16 parce qu'elles utilisent
des techniques uniques. Peut-être que quelqu'un peut les utiliser pour attaquer
les hexamagiques d'ordre 27."
Retour à la page d'accueil http://www.multimagie.com