Cubes magiques multiplicatifs

• Dans cette page:
• Qu'est-ce qu'un cube magique multiplicatif ? (avec la table des meilleurs cubes connus)
• Cubes magiques multiplicatifs d'ordre 3
• Cubes magiques multiplicatifs d'ordre 4
• Cubes magiques multiplicatifs d'ordre 5
• Cubes magiques multiplicatifs d'ordre 6
• Cubes magiques multiplicatifs d'ordre 7
• Cubes magiques multiplicatifs d'ordre 8 à 11
• Dans une autre page :
• Cubes magiques multiplicatifs pandiagonaux parfaits

Qu'est-ce qu'un cube magique multiplicatif ?

Un cube magique multiplicatif est un cube qui est magique en utilisant la multiplication au lieu de l'addition. Les nombres utilisés ne peuvent pas être consécutifs, mais doivent être distincts. Un rappel de quelques définitions, similaires aux cubes additifs :

• un cube semi-magique a toutes ses lignes, colonnes et piles qui sont magiques
• un cube magique a toutes ses lignes, colonnes, piles et triagonales (= les 4 grandes diagonales) qui sont magiques
• un cube magique parfait a toutes ses lignes, colonnes, piles, triagonales et petites diagonales (= diagonales des carrés parallèles aux faces) qui sont magiques
• un cube magique pandiagonal parfait a toutes ses lignes, colonnes, piles, triagonales, diagonales, triagonales brisées et diagonales brisées qui sont magiques

Il semble que les premiers cubes magiques multiplicatifs aient été publiés en 1913 par Harry A. Sayles dans The Monist en 1913. Cet article a été republié dans le livre Magic squares and cubes de W.S. Andrews, où l'on peut trouver (page 293) deux cubes :

• un cube d'ordre 3, avec le produit magique = P = 27000, et avec le nombre maximum utilisé = Nb max = 900
• un cube d'ordre 4, P = 57153600, Nb max = 7560

1913 : premier cube magique multiplicatif,
par H. A. Sayles. P = 27000, Nb max = 900.

1	90	300		150	4	45		180	75	2
60	25	18		9	30	100		50	36	15
450	12	5		20	225	6		3	10	900

(cliquer sur l'image pour agrandir le cube)

En 2002, Marián Trenkler, Slovaquie, a publié un article sur les carrés et cubes magiques multiplicatifs dans Obzory Matematiky, Fyziky a Informatiky 1/2002 (31), pages 9-16, avec :

• un cube d'ordre 3, P = 27000, Nb max = 900 (même ensemble de 27 nombres que le cube de Sayles, mais placés différemment)
• un cube d'ordre 4, P = 57153600, Nb max = 7560 (même ensemble de 64 nombres que le cube de Sayles, mais placés différemment)
• un cube d'ordre 5, P = 35286451200, Nb max = 2448

Est-il possible de faire mieux ? Cubes des mêmes ordres, mais utilisant des plus petits produits P, ou des plus petits Nb max ? Oui, à la fois pour l'ordre 4 et 5 !

Après les carrés magiques multiplicatifs, voici les meilleurs cubes connus, d'ordre 3 à 11. Le but est toujours de minimiser le produit magique et le nb max.

Meilleurs cubes magiques multiplicatifs connus (meilleurs connus = avec les plus petits P et/ou Nb max connus)

Ordre	Produit magique P	Nb max	Cube multiplicatif	Commentaires
3	(c) 6 720	160	semi-magique
	(c) 15 120	105
	(a) 27 000	900	magique	Le meilleur cube magique connu (de tout ordre) utilisant le plus petit P
	216 000	400
4	(b) 4 324 320	351	magique	Le meilleur cube magique connu (de tout ordre) utilisant le plus petit Nb max
5	(b) 13 967 553 600	855	magique	+ triagonales brisées magiques
	(b) 101 625 502 003 200 000	2 976 750	magique parfait	Le meilleur cube magique parfait connu (de tout ordre) utilisant le plus petit P
	(b) 104 064 514 051 276 800 000	250 880
6	115 651 343 808 000	3 300	semi-magique
	223 592 598 028 800	2 262
	(b) 117 327 450 240 000	5 225	magique
	(b) 23 959 607 303 503 872 000	849 420	magique parfait
	(b) 80 863 674 649 325 568 000 000	66 924
7	(b) 897 612 484 786 617 600	3 367	magique	+ triagonales brisées magiques
	(b) 19 407 837 508 899 840 000	2 912		+ triagonales brisées magiques
	1 411 407 979 783 492 239 360 000 000	1 259 712	magique parfait
	5 750 476 043 814 094 602 240 000 000	862 400
8	(c) 13 248 760 275 450 475 776 000	4 797	magique
	89 518 183 823 250 314 294 722 560 000	17 297 280	magique pandiag. parfait (*)	Le meilleur cube magique pandiag. parfait connu (de tout ordre) utilisant le plus petit P
9	(c) 321 308 934 200 224 938 519 552 000	7 191	magique
	265 237 261 271 449 982 022 984 892 416 000	591 192	magique pandiag. parfait (*)
10	117 218 854 345 145 394 654 241 228 800 000	22 125	semi-magique
	602 839 822 346 462 029 650 383 462 400 000	17 400
	(c) 2 108 555 793 636 163 874 695 070 438 860 800 000	568 875	magique
	(c) 23 827 892 281 763 155 326 511 017 263 976 960 000	511 270
	(b) ~  2.62 E+51	1 920 996 000	magique parfait
	(b) ~  3.52 E+59	9 018 009 000	magique pandiag. parfait (*)
11	(c) 386 505 025 119 121 838 921 061 678 274 867 200 000	20 801	magique
	9 009 441 144 967 875 033 124 980 845 568 000 000	46 620	magique pandiag. parfait (*)
	174 930 251 129 029 312 377 859 321 968 844 800 000	24 992		Le meilleur cube magique parfait connu (de tout ordre), et le meilleur cube magique pandiag. parfait connu (de tout ordre) utilisant le plus petit Nb max

• Cubes de cette table trouvés en 2006 par Christian Boyer, sauf (a) trouvé en 1913 par Harry Sayles, (b) en 2010-2012-2013 par Toshihiro Shirakawa, (c) en 2017 by Elbert Krison
• (*) Voir la page sur les cubes magiques multiplicatifs pandiagonaux parfaits
• Si vous réussissez à obtenir de plus petits produits (ou de plus petits nbs max), envoyez-moi un message ! Je serai heureux d'ajouter vos résultats dans ce site.

• Télécharger les meilleurs cubes multiplicatifs, ordres 3 à 7 (fichier Excel de 146Ko)
• Télécharger les meilleurs cubes multiplicatifs, ordres 8 à 11 (fichier Excel de 276Kb)

Cubes magiques multiplicatifs d'ordre 3

Il est facile de prouver que tout cube magique multiplicatif d'ordre 3 doit avoir P = (centre)^3. Avec les deux constructions différentes possibles utilisant l'entier 1

Deux cubes magiques multiplicatifs,
P =centre³ = a³b³c³, Nb max = a²b²c²

1	abc²	a²b²c		a	a²bc²	b²c
ab²c	a²	bc²		a²b²c	1	abc²
a²bc²	b²c	a		bc²	ab²c	a²
a²bc	b²	ac²		a²bc	b²	ac²
c²	abc	a²b²		c²	abc	a²b²
ab²	a²c²	bc		ab²	a²c²	bc
ab²c²	a²c	b		b²c²	ac	a²b
a²b	b²c²	ac		ab	a²b²c²	c
c	ab	a²b²c²		a²c	b	ab²c²

on peut produire exactement 4 cubes magiques multiplicatifs différents d'ordre 3 avec le même P = (2·3·5)^3 = 27000 : un cube avec la première construction, et trois avec la seconde construction. Ils utilisent le même jeu d'entiers, mais ils sont "différents" car à partir de n'importe lequel de ces 4 cubes, il est impossible d'obtenir l'un des 3 autres en utilisant uniquement des symétries et rotations.

Les 4 plus petits cubes magiques multiplicatifs différents d'ordre 3,
P = 30³ = 27000,       Nb max = 30² = 900.
Celui de gauche est le cube de Sayles, celui de droite est celui de Trenkler.

1	150	180		2	300	45		3	450	20		5	450	12
90	4	75		180	1	150		180	1	150		300	1	90
300	45	2		75	90	4		50	60	9		18	60	25
60	9	50		60	9	50		90	4	75		150	4	45
25	30	36		25	30	36		25	30	36		9	30	100
18	100	15		18	100	15		12	225	10		20	225	6
450	20	3		225	10	12		100	15	18		36	15	50
12	225	10		6	900	5		6	900	5		10	900	3
5	6	900		20	3	450		45	2	300		75	2	180

Il est impossible de construire de meilleurs cubes d'ordre 3 avec un plus petit P. Mais, en utilisant Min nb > 1, il est possible de construire des cubes d'ordre 3 avec des plus petits Nb max (et plus gros P), le plus petit Nb max possible étant 400. Voici quelques exemples avec Nb max < 900 :

A gauche, P = 60³ = 216000, Nb max = 400.
Au milieu, P = 120³ = 1728000, Nb max = 480.
A droite, P = 120³ = 1728000, Nb max = 576.

90	80	30		320	150	36		200	192	45
240	9	100		180	32	300		288	25	240
10	300	72		30	360	160		30	360	160
48	225	20		60	288	100		96	225	80
25	60	144		200	120	72		100	120	144
180	16	75		144	50	240		180	64	150
50	12	360		90	40	480		90	40	480
36	400	15		48	450	80		60	576	50
120	45	40		400	96	45		320	75	72

Et il est possible de construire des cubes semi-magiques d'ordre 3 utilisant des constantes plus petites. Dans les trois exemples ci-dessous, toutes les lignes, colonnes et piles ont le même produit magique P = 7560, mais quelques-unes de leurs 4 triagonales n'ont pas le même produit : l'exemple de droite est un cube quasi magique, puisque seulement une triagonale est incorrecte !!!

Trois cubes semi-magiques avec le même P = 7560,
Nbs max = 135 (gauche), 180 (milieu), 252 (droite).
Une, deux et trois triagonales correctes.

1	56	135		1	42	180		1	30	252
72	15	7		54	20	7		90	28	3
105	9	8		140	9	6		84	9	10
84	45	2		84	45	2		60	63	2
5	14	108		5	14	108		7	6	180
18	12	35		18	12	35		18	20	21
90	3	28		90	4	21		126	4	15
21	36	10		28	27	10		12	45	14
4	70	27		3	70	36		5	42	36

En février 2013, André LFS Bacci, Brasilia, Brésil, a construit ce cube semi-magique avec un plus petit P :

P = 6720,
Nb max = 224,
Une triagonale

21	20	16
32	42	5
10	8	84
2	56	60
15	4	112
224	30	1
160	6	7
14	40	12
3	28	80

En juin 2017, j'étais surpris de recevoir des cubes semi-magiques d'ordre 3 encore meilleurs ! De Elbert Krison, un jeune écolier de 15 ans de Djakarta, Indonésie. Elbert a aussi envoyé de nouveaux meilleurs cubes pour les ordres 8 à 11 listés dans la table.

P = 6720, Nb max = 160 (gauche)
P = 15120, Nb max = 105 (droite)
Une triagonale

3	28	80		8	105	18
160	6	7		21	48	15
14	40	12		90	3	56
16	5	84		30	6	84
21	32	10		12	35	36
20	42	8		42	72	5
140	48	1		63	24	10
2	35	96		60	9	28
24	4	70		4	70	54

Et ajouter des diagonales magiques ? Pour les cubes multiplicatifs, comme pour les additifs, il est impossible de construire des cubes magiques parfaits d'ordre 3.

Cubes magiques multiplicatifs d'ordre 4

Le cube de Sayles et le cube de Trenkler ont les mêmes caractéristiques : P = 57153600, Nb max = 7560. Est-il possible de construire des cubes d'ordre 4 avec des constantes plus petites ? Oui ! Mes meilleurs cubes ont un P plus de 8 fois plus petit, et un Nb max plus de 18 fois plus petit :

Cubes magiques multiplicatifs d'ordre 4, par Christian Boyer
P = 6 486 480 et Nb max = 546 (cube de gauche, janvier 2006),
P = 17 297 280 et Nb max = 364 (cube de droite, juin 2007)
(cliquer sur l'image pour agrandir un cube)

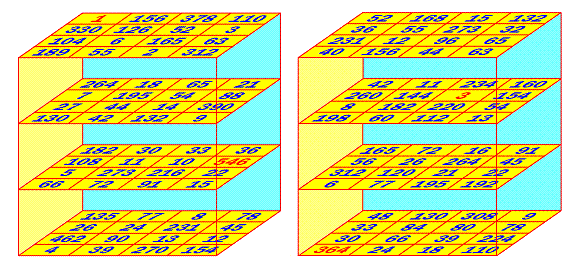
Quelques diagonales de mes deux cubes sont magiques, mais pas toutes : à la fois pour les cubes additifs et les cubes multiplicatifs, il est impossible de construire des cubes magiques parfaits d'ordre 4.

C'étaient mes deux meilleurs cubes, mais je je n'était pas sûr d'avoir trouvé les meilleurs cubes possibles. C'est pourquoi je posais ces questions suivantes. Qui saura construire de meilleurs cubes d'ordre 4 (avec un plus petit P ou un plus petit Nb max) ? Est-il possible de construire un cube magique multiplicatif (de tout ordre !) utilisant des entiers < 364 ? De tout ordre, car on peut remarquer que le Nb max = 364 du cube de droite d'ordre 4 est plus petit que le Nb max = 400 utilisé pour les meilleurs cubes d'ordre 3.

En juillet 2008, Michael Quist a travaillé sur cette énigme #5, et trouvé que tout cube d'ordre 4 doit avoir Nb max ≥ 221 et que tout cube d'ordre 5 (ou plus) doit avoir Nb max ≥ 442. Si l'on suppose que son travail est correct (le lire en anglais ici), et si l'on suppose que tout cube d'ordre 3 doit avoir Nb max ≥ 400, alors le problème se limite à l'ordre 4, et est équivalent à : est-il possible de construire un cube magique multiplicatif, donc d'ordre 4, et ayant 221 ≤ Nb max < 364 ?

En janvier 2010, Max Alekseyev, Dept of Computer Science & Engineering, University of South Carolina, a trouvé un autre cube magique d'ordre 4 ayant le même Nb max = 364 que mon cube ci-dessus, mais avec un P plus petit. Aucune de ses 24 petites diagonales ne sont magiques (8 petites diagonales sont magiques dans mon cube), mais ce n'est pas un problème puisque cela n'est pas demandé dans un cube magique : seulement les lignes + colonnes + piles + 4 triagonales doivent être magiques. Un excellent cube construit par Max !

Janvier 2010 : Cube magique multiplicatif
par Max Alekseyev,
Nb max = 364,
P = 8 648 640

1	110	224	351
130	8	297	28
308	27	13	80
216	364	10	11
231	12	78	40
96	273	5	66
6	55	168	156
65	48	132	21
144	91	15	44
77	18	52	120
195	32	198	7
4	165	56	234
260	72	33	14
9	220	112	39
24	182	20	99
154	3	117	160

Toshiro Shirakawa en 2010 (Kuwana, Japon, 1983 - )

Et finalement en avril 2010, Toshihiro Shirakawa a résolu mon énigme #5 avec cet excellent cube utilisant des plus petits entiers: Max nb = 351 < 364. Le produit magique est aussi plus petit que les cubes précédents. Félicitations !!! Toshihiro habite à Ebina Kanagawa, Japon. Il est programmeur, et a comme hobby les mathématiques.

Avril 2010. Meilleur cube magique multiplicatif connu d'ordre 4, par Toshihiro Shirakawa
et meilleur cube connu -de tous les ordres- utilisant les plus petits entiers possibles
P = 4 324 320 et Nb max = 351
(cliquer sur l'image pour l'agrandir)
 

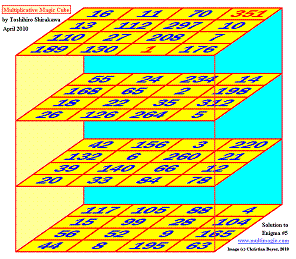
Sa méthode est facile et ingénieuse, sans aucune programmation informatique. Il a utilisé, directement depuis ce site web, mon propre carré semi-magique multiplicatif 4x4 ayant le plus petit produit possible que j'avais construit en 2005, avec le produit magique 4320 = 2⁵ * 3³ * 5 et Nb max 27 :

16	1	10	27	=	1A	1B	1C	1D
5	24	18	2		2A	2B	2C	2D
6	12	3	20		3A	3B	3C	3D
9	15	8	4		4A	4B	4C	4D

Remarquant que ce carré utilise seulement les facteurs 2, 3 et 5, il l'a intelligemment combiné avec les quatre facteurs (E, F, G, H) = (1, 11, 7, 13). C'est pourquoi son produit magique est 4320(du carré) *7*11*13(ses facteurs) = 4324320, et son Nb max est 27(du carré) * 13(son facteur max) = 351. Et 351 est inférieur à 364, comme demandé dans l'énigme. Et voilà ! Euh... honte à moi... d'avoir été incapable de penser à cette méthode inégnieuse.. utilisant mon propre carré...

1A	1B	1C	1D	*	E	F	G	H
1B	1A	1D	1C		H	G	F	E
1C	1D	1A	1B		F	E	H	G
1D	1C	1B	1A		G	H	E	F
2A	2B	2C	2D		F	E	H	G
2B	2A	2D	2C		G	H	E	F
2C	2D	2A	2B		E	F	G	H
2D	2C	2B	2A		H	G	F	E
3A	3B	3C	3D		G	H	E	F
3B	3A	3D	3C		F	E	H	G
3C	3D	3A	3B		H	G	F	E
3D	3C	3B	3A		E	F	G	H
4A	4B	4C	4D		H	G	F	E
4B	4A	4D	4C		E	F	G	H
4C	4D	4A	4B		G	H	E	F
4D	4C	4B	4A		F	E	H	G

Je peux maintenant donner la méthode utilisée pour mon cube (P, NbMax) = (17297280, 364) qui était à battre avec l'énigme #5. Ce cube était construit à partir du cube eulérien (ou gréco-latin) ci-dessous, utilisant le meilleur ensemble possible (A, B, C, D) (I, J, K, L) (a, b, c, d) générant 64 entiers distincts et générant le plus petit NbMax :

• (A, B, C, D) = (1, 2, 3, 4)
• (I, J, K, L) = (1, 5, 6, 7)
• (a, b, c, d) = (3, 8, 11, 13)
   

D

C

A

B

*

I

L

J

K

*

d

b

a

c

B

A

C

D

K

J

L

I

a

c

d

b

C

D

B

A

L

I

K

J

c

a

b

d

A

B

D

C

J

K

I

L

b

d

c

a

B

A

C

D

L

I

K

J

a

c

d

b

D

C

A

B

J

K

I

L

d

b

a

c

A

B

D

C

I

L

J

K

b

d

c

a

C

D

B

A

K

J

L

I

c

a

b

d

C

D

B

A

J

K

I

L

c

a

b

d

A

B

D

C

L

I

K

J

b

d

c

a

D

C

A

B

K

J

L

I

d

b

a

c

B

A

C

D

I

L

J

K

a

c

d

b

A

B

D

C

K

J

L

I

b

d

c

a

C

D

B

A

I

L

J

K

c

a

b

d

B

A

C

D

J

K

I

L

a

c

d

b

D

C

A

B

L

I

K

J

d

b

a

c

Mon autre cube (P, NbMax) = (6486480, 546) utilise un cube eulérien similaire, mais avec le meilleur ensemble possible générant 64 entiers distinct et générant le plus petit produit : (1, 2, 3, 6), (1, 4, 5, 7), (1, 9, 11, 13).

Cubes magiques multiplicatifs d'ordre 5

Le cube de Trenkler publié en 2002 a son produit P = 35286451200, et son Nb max = 2448. Est-il possible construire des cubes d'ordre 5 avec des constantes plus petites ? Oui ! Mon meilleur cube a un P plus de 2 fois plus petit, et un Nb max plus de 2 fois plus petit :

Janvier 2006 : cube magique multiplicatif d'ordre 5, par Christian Boyer
P = 16 761 064 320 et Nb max = 1026
(cliquer sur l'image pour l'agrandir)
 

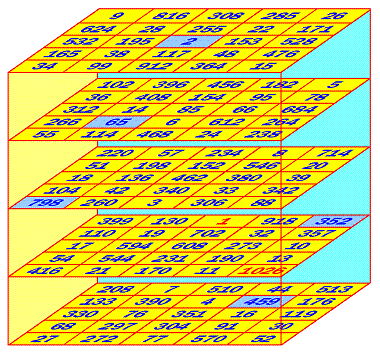
Toutes ses lignes, colonnes, piles et 4 triagonales sont magiques. Et ce cube a une très belle caractéristique supplémentaire : toutes ses triagonales brisées sont magiques, comme par exemple celle en fond bleu.

En mai 2010, Toshihiro Shirakawa a construit un cube magique multiplicatif avec des plus petites caractéristiques : P = 13 967 553 600 et Nb max = 855. Aussi avec des triagonales brisées magiques. C'est aujourd'hui le meilleur cube magique connu d'ordre 5 ! Vous pouvez le voir dans fichier Excel téléchargeable, sous la table. D'une façon similaire à sa méthode d'ordre 4, il a utilisé mon carré magique multiplicatif d'ordre 5 (reproduit dessous), combiné avec (1, 11, 13, 17, 19). Mon cube était un cube eulérien avec (1, 2, 3, 4, 6) (1, 5, 7, 8, 9) (1, 11, 13, 17, 19).

12	35	1	40	18
36	2	24	7	25
14	45	15	4	8
5	16	42	30	3
10	6	20	9	28

Hélas les diagonales de nos deux cubes ne sont pas magiques : ce ne sont pas des cubes magiques parfaits. Il est toutefois possible de construire des cubes magiques parfaits d'ordre 5 : utilisez le premier cube magique (additif) parfait d'ordre 5 construit par Walter Trump et moi-même en 2003, et remplacez chaque nombre n par 2^(n-1). Vous obtenez alors un cube magique parfait multiplicatif... mais très stupide... utilisant des très grands nombres : Nb max = 2^(125-1) = 2,13 · 10^37, et P = 2^310 = 2,09 · 10^93. En décembre 2012, Toshihiro Shirakawa a construit deux cubes magiques parfaits d'ordre 5 bien meilleurs : un avec Max nb = 250 880, un avec P = 2520^5 = 1.01 · 10^17. Etonnant, mais avec un ordre plus grand, des cubes parfaits utilisant des plus petits entiers sont connus : voir mon cube parfait pandiagonal d'ordre 11 avec Nb max = 24 992 < 250 880.

Cubes magiques multiplicatifs d'ordre 6

En janvier 2006, j'ai construit deux cubes:

• P = 115 651 343 808 000, Nb max = 3 300
• P = 223 592 598 028 800, Nb max = 2 262

Ces cubes sont seulement semi-magiques : leurs 4 triagonales ne sont pas magiques.

Ensuite, en mai 2006, j'ai construit un cube magique avec cette fois 4 triagonales magiques. Cette caractéristique supplémentaire a un coût, plus gros P et Nb max que les cubes semi-magiques précédents :

• P = 170 400 029 184 000 000, Nb max = 554 400

Puis en juin 2010, Toshihiro Shirakawa a construit un cube magique avec de bien plus petites caractéristiques que mon pauvre cube ci-dessus :

• P = 117 327 450 240 000, Nb max = 5 225

C'est aujourd'hui le meilleur cube connu d'ordre 6 !

Il est possible de construire des cubes magiques parfaits d'ordre 6 : utilisez le premier cube magique (additif) parfait d'ordre 6 construit par Walter Trump en 2003, et remplacez chaque nombre n par 2^(n-1). Vous obtenez alors un cube magique parfait multiplicatif... mais très stupide... utilisant des très grands nombres : Nb max = 2^(216-1) = 5,27 · 10^64, et P = 2^645 = 1,46 · 10^194. En décembre 2012 et février 2013, Toshihiro Shirakawa a construit deux cubes magiques parfaits d'ordre 6 bien meilleurs : un avec Max nb = 66 924, un avec P = 2 882 880^3 = 2.39 · 10^19. Etonnant, mais avec un ordre plus grand, des cubes parfaits utilisant des plus petits entiers sont connus : voir mon cube parfait pandiagonal d'ordre 11 avec Nb max = 24 992 < 66 924.

Cubes magiques multiplicatifs d'ordre 7

En janvier 2006, mes deux meilleurs cubes étaient :

• P = 1 663 528 929 334 272 000, Nb max = 5 952
• P = 3 881 567 501 779 968 000, Nb max = 4 352

Mais en mai 2010, Toshihiro Shirakawa a construit de meilleurs cubes :

• P = 897 612 484 786 617 600, Nb max = 3 367
• P = 19 407 837 508 899 840 000, Nb max = 2 912

Comme le cube magique d'ordre 5 vu plus haut, toutes leurs triagonales brisées et 4 triagonales entières sont magiques, mais leurs diagonales ne sont pas magiques : ce ne sont pas des cubes magiques parfaits. Avec les mêmes P et Nbs max, j'ai réussi à construire des cubes ayant toutes leur diagonales magiques... mais tout en perdant hélas 2 triagonales magiques sur les 4 triagonales.

En gardant les diagonales magiques, j'ai construit deux cubes avec 3 triagonales magiques (maintenant, seulement une triagonale est mauvaise !) mais avec le coût d'utiliser des plus grandes constantes :

• P = 16 579 776 648 314 880 000, Nb max = 24 000
• P = 101 059 382 457 057 024 000, Nb max = 9 486

et finalement réussi à construire des cubes magiques parfaits avec 4 triagonales magiques, mais avec d'encore plus grandes constantes. Le coût pour obtenir la 4ème triagonale est très élevé !

• P = 1 411 407 979 783 492 239 360 000 000, Nb max = 1 259 712
• P = 5 750 476 043 814 094 602 240 000 000, Nb max = 862 400

Cubes magiques multiplicatifs d'ordre 8 à 11

Voir le résumé dans la table au début de cette page. Et voir la page sur les cubes magiques multiplicatifs pandiagonaux parfaits.

En souvenir de janvier 2006, date à laquelle ces cubes ont été créés, les deux premiers nombres utilisés dans les cubes d'ordre 10 et 11 sont : "2006" et "1" !

Retour à la page d'accueil http://www.multimagie.com