Enigmes sur les Carrés Magiques : gagnez 8.000€ et 12 bouteilles de champagne !!!

Alors que les carrés magiques sont connus et étudiés depuis de longs siècles, il est étonnant que l’on ne sache toujours pas aujourd’hui, pour certains types de carrés magiques, quels sont les plus petits carrés possibles ! Aussi, pour faire avancer ces problèmes encore non résolus, douze prix totalisant 8.000€ + 12 bouteilles de champagne sont offerts pour les solutions à douze énigmes (six grandes de 1.000€ chacune, et six petites de 100 à 500€ chacune) :

Après la résolution des énigmes #3a, #4c, #5 et #6b, il reste encore huit prix totalisant 6.500€ + huit bouteilles de champagne (au moment de la dernière mise à jour de ce site). Toutes les énigmes sur les carrés 7x7 étant maintenant résolues, les énigmes restantes sont sur des petits carrés, de 3x3 à 6x6.

Qui pourra construire, ou prouver l'impossibilité :

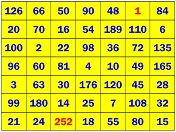
  1. carré magique 3x3 utilisant 7 (ou pourquoi pas 8, ou 9) entiers carrés distincts différent de ce seul exemple connu (et de ses rotations, symétries et multiples k²) :

      2. 373²

      289²

      565²

      360721

      425²

      23²

      205²

      527²

      222121
  2. carré bimagique 5x5 utilisant des entiers positifs distincts
  3. carré semi-magique 3x3 de cubes utilisant des entiers positifs distincts élevés au cube (petite énigme #3a : carré 7x7)
  4. carré magique 4x4 de cubes utilisant des entiers positifs distincts élevés au cube (petites énigmes #4a, #4b, #4c : carrés 5x5, 6x6, 7x7)
  5. cube magique multiplicatif utilisant des entiers positifs distincts < 364
  6. carré magique additif-multiplicatif 5x5 utilisant des entiers positifs distincts (petites énigmes #6a , #6b : carrés 6x6, 7x7)

Non, je n'ai pas moi-même les solutions... Bien sûr, seul le premier qui résoudra une énigme remportera le prix associé et aura son nom ajouté dans ce tableau :

Remarque importante sur la grande énigme #1. Strictement parlant, une preuve d'impossibilité de 8 ou 9 entiers carrés dans un carré magique 3x3 n'est pas une solution, puisqu'un autre carré magique utilisant 7 entiers carrés resterait (peut-être) possible. Toutefois, puisqu'une telle preuve d'impossibilité serait un résultat impressionnant, il serait récompensé par un prix : 500€ + bouteille de champagne.

Gagnants
  • Bravo à Toshihiro Shirakawa, Japon, qui a été très rapide après l'annonce du concours effectuée le 6 avril 2010. Il a résolu deux énigmes:
    #5 dès le 15 avril 2010 avec son cube, puis #3a une semaine plus tard, le 22 avril, avec son carré

    • Le voici heureux, avec sa première bouteille de champagne ! Il en a reçu une seconde, quelques jours plus tard. Un total de deux bouteilles Moët & Chandon impérial et de 1100€.

 

 

 
  • Bravo à Sébastien Miquel, France, qui a résolu l'énigme #4c le 20 février 2015
    avec son carré 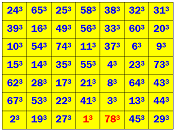, et a donc gagné une bouteille et 200€.


C. Boyer & S. Miquel
(Paris, mars 2015)

 

 

  • Un an et demi plus tard, bravo encore à Sébastien Miquel, qui a résolu l'énigme #6b le 15 août 2016
    avec son carré , et a donc gagné à nouveau une bouteille et 200€.

    • Qui sera le gagnant suivant ? Avec quelle énigme ?


C. Boyer & S. Miquel
(Paris, septembre 2016)

Enigmes dans Pour La Science... et ailleurs

                                        dans
Dossier Pour La Science (Jeux math')....... et site Pour La Science

Un gros merci aux nombreuses personnes, journaux et sites qui ont ensuite relayé le concours après l'envoi du communiqué de presse le 6 avril 2010, notamment, par ordre chronologique :

Par avance, mes excuses aux autres dont je n'ai pas eu connaissance, mais je les remercie aussi !

Et aussi merci à, pour leur annonce des solutions trouvées par Toshihiro Shirakawa:

Avec cet article en japonais dans Sugaku Seminar, je sais maintenant que mon nom s'écrit de cette façon en katakana :

Merci Toshihiro pour m'avoir détaillé ces caractères de mon nom. Amusant : les nombres étant les seuls caractères que l'on peut facilement lire, on peut déduire que ce paragraphe dit probablement qu'en 2010, en avril (4), j'ai soumis 12 énigmes, prix totalisant 8000 euros, chacun étant de 100 à 1000 euros. Ai-je vrai ?

Merci pour leur annonce de la solution #4c trouvée par Sébastien Miquel :

Merci pour leur annonce de la solution #6b trouvée par Sébastien Miquel :

Retour à la page d'accueil http://www.multimagie.com